Advertisements
Advertisements
Question
A man has fallen into a ditch of width d and two of his friends are slowly pulling him out using a light rope and two fixed pulleys as shown in the following figure. Show that the force (assumed equal for both the friends) exerted by each friend on the road increases as the man moves up. Find the force when the man is at a depth h.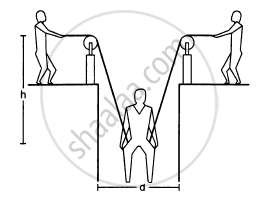
Solution
(a) At any depth, let the ropes makes an angle θ with the vertical.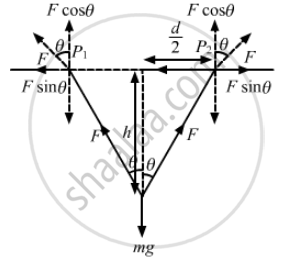
From the free-body diagram,
Fcosθ + Fcosθ − mg = 0
2Fcosθ = mg
\[\Rightarrow F = \frac{mg}{2cos\theta}\]
As the man moves up, θ increases, i.e. cosθ decreases. Thus, F increases.
\[\cos\theta = \frac{h}{\sqrt{\left( d/2 \right)^2 + h^2}}\]
(b) When the man is at depth h,
\[F = \frac{mg}{2\cos\theta}\]
\[ = \frac{mg}{2\left[ h/\sqrt{\left( \frac{d}{2} \right)^2 + h^2} \right]}\]
\[ = \frac{mg}{4h}\sqrt{d^2 + 4 h^2}\]
APPEARS IN
RELATED QUESTIONS
A man of mass 70 kg stands on a weighing scale in a lift which is moving
- upwards with a uniform speed of 10 m s-1
- downwards with a uniform acceleration of 5 m s–2
- upwards with a uniform acceleration of 5 m s–2. What would be the readings on the scale in each case?
- What would be the reading if the lift mechanism failed and it hurtled down freely under gravity?
A helicopter of mass 1000 kg rises with a vertical acceleration of 15 m s–2. The crew and the passengers weigh 300 kg. Give the magnitude and direction of the
(a) force on the floor by the crew and passengers,
(b) action of the rotor of the helicopter on the surrounding air,
(c) force on the helicopter due to the surrounding air.
The rear side of a truck is open and a box of 40 kg mass is placed 5 m away from the open end as shown in Figure. The coefficient of friction between the box and the surface below it is 0.15. On a straight road, the truck starts from rest and accelerates with 2 m s–2. At what distance from the starting point does the box fall off the truck? (Ignore the size of the box).

You are travelling in a car. The driver suddenly applies the brakes and you are pushed forward. Why does this happen?
A spy jumps from an airplane with his parachute. The spy accelerates downward for some time when the parachute opens. The acceleration is suddenly checked and the spy slowly falls to the ground. Explain the action of the parachute in checking the acceleration.
If the tension in the cable supporting an elevator is equal to the weight of the elevator, the elevator may be
(a) going up with increasing speed
(b) going down with increasing speed
(c) going up with uniform speed
(d) going down with uniform speed
Two blocks of equal mass m are tied to each other through a light string. One of the blocks is pulled along the line joining them with a constant force F. Find the tension in the string joining the blocks.
An empty plastic box of mass m is found to accelerate up at the rate of g/6 when placed deep inside water. How much sand should be put inside the box so that it may accelerate down at the rate of g/6?
Consider the Atwood machine of the previous problem. The larger mass is stopped for a moment, 2.0 s after the system is set into motion. Find the time that elapses before the string is tight again.
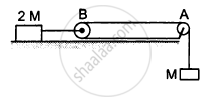
Consider the situation shown in the following figure. Both the pulleys and the string are light and all the surfaces are frictionless. (a) Find the acceleration of the mass M; (b) find the tension in the string; (c) calculate the force exerted by the clamp on the pulley A in the figure.
Two balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare:
(i) Their inertia.
(ii) Their momentum.
(iii) The force needed to stop them in the same time.
State the Newton's second law of motion. What information do you get from it?
Calculate the magnitude of force which when applied on a body of mass 0.5 kg produces an acceleration of 5 m s-2.
Calculate the velocity of a body of mass 0.5 kg, when it has a linear momentum of 5 Ns.
Define Newton’s second law of motion.
Prove mathematically F = ma
ame the law of motion which gives the definition of force.
A stone is thrown vertically upward with a velocity of 9.8 m/s. When will it reach the ground?
A cricket ball of mass 150 g has an initial velocity `u = (3hati + 4hatj)` m s−1 and a final velocity `v = - (3hati + 4hatj)` m s−1 after being hit. The change in momentum (final momentum-initial momentum) is (in kg m s1)
