Advertisements
Advertisements
Question
In the following figure, m1 = 5 kg, m2 = 2 kg and F = 1 N. Find the acceleration of either block. Describe the motion of m1 if the string breaks but F continues to act.
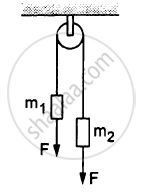
Solution
Let the acceleration of the blocks be a.
The free-body diagrams for both the blocks are shown below: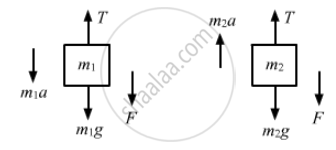
From the free-body diagram,
m1a = m1g + F − T ...(i)
Again, from the free-body diagram,
m2a = T − m2g − F ...(ii)
Adding equations (i) and (ii), we have:
\[a = g\frac{m_1 - m_2}{m_1 + m_2}\]
\[\Rightarrow a = \frac{3g}{7} = \frac{29 . 4}{7}\]
\[ = 4 . 2 m/ s^2\]
After the string breaks, m1 moves downward with force F acting downward. Then,
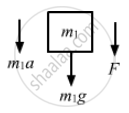
m1a = F + m1g
5a = 1 + 5g
\[\Rightarrow a = \frac{5g + 1}{5}\]
\[ = g + 0 . 2 m/ s^2\]
APPEARS IN
RELATED QUESTIONS
A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of 15 ms–1. How long does the body take to stop?
Two bodies of masses 10 kg and 20 kg respectively kept on a smooth, horizontal surface are tied to the ends of a light string. A horizontal force F = 600 N is applied to
- A,
- B along the direction of string. What is the tension in the string in each case?
Explain why a cricketer moves his hands backwards while holding a catch.
A block of mass 15 kg is placed on a long trolley. The coefficient of static friction between the block and the trolley is 0.18. The trolley accelerates from rest with 0.5 ms–2 for 20 s and then moves with uniform velocity. Discuss the motion of the block as viewed by (a) a stationary observer on the ground, (b) an observer moving with the trolley.
A free 238U nucleus kept in a train emits an alpha particle. When the train is stationary, a nucleus decays and a passenger measures that the separation between the alpha particle and the recoiling nucleus becomes x at time t after the decay. If the decay takes place while the train is moving at a uniform velocity v, the distance between the alpha particle and the recoiling nucleus at a time t after the decay, as measured by the passenger, is
A person says that he measured the acceleration of a particle to be non-zero even though no force was acting on the particle.
A block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block by another string. Find the tensions in the two strings. Take g = 10 m/s2.
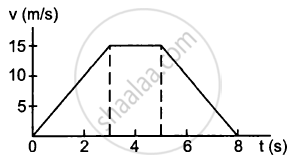
A particle of mass 50 g moves in a straight line. The variation of speed with time is shown in the following figure. Find the force acting on the particle at t = 2, 4 and 6 seconds.
A small block B is placed on another block A of mass 5 kg and length 20 cm. Initially, the block B is near the right end of block A (In the following Figure). A constant horizontal force of 10 N is applied to the block A. All the surfaces are assumed frictionless. Find the time that elapses before block B separates from A.

A person is standing on a weighing machine placed on the floor of an elevator. The elevator starts going up with some acceleration, moves with uniform velocity for a while and finally decelerates to stop. The maximum and the minimum weights recorded are 72 kg and 60 kg, respectively. Assuming that the magnitudes of acceleration and deceleration are the same, find (a) the true weight of the person and (b) the magnitude of the acceleration. Take g = 9.9 m/s2.
Find the reading of the spring balance shown in the following figure. The elevator is going up with an acceleration g/10, the pulley and the string are light and the pulley is smooth.

Consider the Atwood machine of the previous problem. The larger mass is stopped for a moment, 2.0 s after the system is set into motion. Find the time that elapses before the string is tight again.
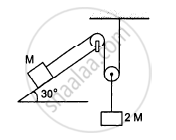
Find the acceleration of the block of mass M in the situation shown in the following figure. All the surfaces are frictionless and the pulleys and the string are light.
The unit of linear momentum is :
State the magnitude and direction of the force of gravity acting on the body of mass 5 kg. Take g = 9.8 m s-2.
A stone is dropped freely from the top of a tower and it reaches the ground in 4 s. Taking g = 10m s-2, calculate the height of the tower.
Define Newton’s second law of motion.
What do you mean by linear momentum of a body?
A cricket ball of mass 150 g has an initial velocity `u = (3hati + 4hatj)` m s−1 and a final velocity `v = - (3hati + 4hatj)` m s−1 after being hit. The change in momentum (final momentum-initial momentum) is (in kg m s1)
