Advertisements
Advertisements
Question
A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of 15 ms–1. How long does the body take to stop?
Solution 1
Retarding force, F = –50 N
Mass of the body, m = 20 kg
Initial velocity of the body, u = 15 m/s
Final velocity of the body, v = 0
Using Newton’s second law of motion, the acceleration (a) produced in the body can be computed as follows:
F = ma
–50 = 20 × a
`:. a = (-50)/20 = -2.5 "m/s"^2`
The first equation of motion allows for the calculation of the body's time (t) to come to rest as follows:
v = u + at
`:. t = (-u)/a = (-15)/(-2.5) = 6 s`
Solution 2
Here m = 20 kg, F = – 50 N (retardation force)
As F = ma
`=> a = F/m = (-50)/20 = -2.5 ms^(-2)`
Using equation v = u + at
Given `u = 15 ms^(-1), v = 0`
Now, 0 = 15 + (-25) t
or t = 6 s
APPEARS IN
RELATED QUESTIONS
A monkey of mass 40 kg climbs on a rope in given Figure which can stand a maximum tension of 600 N. In which of the following cases will the rope break: the monkey
(a) climbs up with an acceleration of 6 m s–2
(b) climbs down with an acceleration of 4 m s–2
(c) climbs up with a uniform speed of 5 m s–1
(d) falls down the rope nearly freely under gravity?
(Ignore the mass of the rope).

Two blocks of equal mass m are tied to each other through a light string. One of the blocks is pulled along the line joining them with a constant force F. Find the tension in the string joining the blocks.
A force \[\vec{F} = \vec{v} \times \vec{A}\] is exerted on a particle in addition to the force of gravity, where \[\vec{v}\] is the velocity of the particle and \[\vec{A}\] is a constant vector in the horizontal direction. With what minimum speed, a particle of mass m be projected so that it continues to move without being defelected and with a constant velocity?
Consider the Atwood machine of the previous problem. The larger mass is stopped for a moment, 2.0 s after the system is set into motion. Find the time that elapses before the string is tight again.
Find the acceleration of the 500 g block in the following figure.
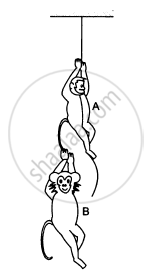
A monkey of mass 15 kg is climbing a rope fixed to a ceiling. If it wishes to go up with an acceleration of 1 m/s2, how much force should it apply on the rope? If the rope is 5 m long and the monkey starts from rest, how much time will it take to reach the ceiling?
A motorcycle of mass 100 kg is running at 10 ms−1. If its engine develops an extra linear momentum of 2000 Ns, calculate the new velocity of a motorcycle.
A hockey player is moving northward and suddenly turns westward with the same speed to avoid an opponent. The force that acts on the player is ______.
Why does a child feel more pain when she falls down on a hard cement floor, than when she falls on the soft muddy ground in the garden?
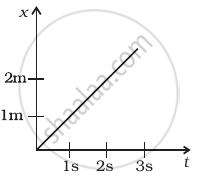
Figure shows (x, t), (y, t ) diagram of a particle moving in 2-dimensions.
|
|
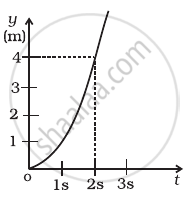 (b) |
If the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle.