Advertisements
Advertisements
प्रश्न
A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of 15 ms–1. How long does the body take to stop?
उत्तर १
Retarding force, F = –50 N
Mass of the body, m = 20 kg
Initial velocity of the body, u = 15 m/s
Final velocity of the body, v = 0
Using Newton’s second law of motion, the acceleration (a) produced in the body can be computed as follows:
F = ma
–50 = 20 × a
`:. a = (-50)/20 = -2.5 "m/s"^2`
The first equation of motion allows for the calculation of the body's time (t) to come to rest as follows:
v = u + at
`:. t = (-u)/a = (-15)/(-2.5) = 6 s`
उत्तर २
Here m = 20 kg, F = – 50 N (retardation force)
As F = ma
`=> a = F/m = (-50)/20 = -2.5 ms^(-2)`
Using equation v = u + at
Given `u = 15 ms^(-1), v = 0`
Now, 0 = 15 + (-25) t
or t = 6 s
APPEARS IN
संबंधित प्रश्न
The below figure shows the position-time graph of a particle of mass 4 kg.
- What is the force on the particle for t < 0, t > 4 s, 0 < t < 4 s?
- What is the impulse at t = 0 and t = 4 s? (Consider one-dimensional motion only.)

A stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are: [Choose the correct alternative]
| Lowest Point | Highest Point | |
| a) | mg – T1 | mg + T2 |
| b) | mg + T1 | mg – T2 |
| c) | `mg + T1 –(m_v_1^2)/R` | mg – T2 + (`mv_1^2`)/R |
| d) | `mg – T1 – (mv)/R` | mg + T2 + (mv_1^2)/R |
T1 and v1 denote the tension and speed at the lowest point. T2 and v2 denote corresponding values at the highest point.
A car accelerates on a horizontal road due to the force exerted by.
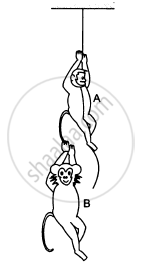
The monkey B, shown in the following figure, is holding on to the tail of monkey A that is climbing up a rope. The masses of monkeys A and B are 5 kg and 2 kg, respectively. If A can tolerate a tension of 30 N in its tail, what force should it apply on the rope in order to carry monkey B with it? Take g = 10 m/s2.
How can Newton's first law of motion be obtained from the second law of motion?
A force acts for 10 s on a stationary body of mass 100 kg, after which the force ceases to act. The body moves through a distance of 100 m in the next 5 s. Calculate : The magnitude of the force
A ball is thrown vertically upwards. It returns 6 s later. Calculate : The greatest height reached by the ball . (Take g = 10 m s-2)
Define Newton’s second law of motion.
What do you mean by linear momentum of a body? A force causes an acceleration of 10 ms-2 in a body of mass 1 kg. What acceleration will be caused by the same force in a body of mass 4 kg?
What do you mean by the conservation of momentum? Briefly, explain the collision between two bodies and the conservation of momentum.
