Advertisements
Advertisements
प्रश्न
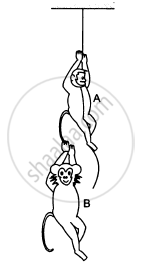
The monkey B, shown in the following figure, is holding on to the tail of monkey A that is climbing up a rope. The masses of monkeys A and B are 5 kg and 2 kg, respectively. If A can tolerate a tension of 30 N in its tail, what force should it apply on the rope in order to carry monkey B with it? Take g = 10 m/s2.
उत्तर
Let the acceleration of monkey A upwards be a, so that a maximum tension of 30 N is produced in its tail.
T − 5g − 30 − 5a = 0 ...(i)
30 − 2g − 2a = 0 ...(ii)
From equations (i) and (ii), we have:
T = 105 N (max.)
and a = 5 m/s2
So, A can apply a maximum force of 105 N on the rope to carry monkey B with it.
For minimum force, there is no acceleration of A and B.
T1 = weight of monkey B
⇒ T1 = 20 N
Rewriting equation (i) for monkey A, we get:
T − 5g − 20 = 0
⇒ T = 70 N
∴ To carry monkey B with it, monkey A should apply a force of magnitude between 70 N and 105 N.
APPEARS IN
संबंधित प्रश्न
A man of mass 70 kg stands on a weighing scale in a lift which is moving
- upwards with a uniform speed of 10 m s-1
- downwards with a uniform acceleration of 5 m s–2
- upwards with a uniform acceleration of 5 m s–2. What would be the readings on the scale in each case?
- What would be the reading if the lift mechanism failed and it hurtled down freely under gravity?
Two bodies of masses 10 kg and 20 kg respectively kept on a smooth, horizontal surface are tied to the ends of a light string. A horizontal force F = 600 N is applied to
- A,
- B along the direction of string. What is the tension in the string in each case?
A batsman deflects a ball by an angle of 45° without changing its initial speed which is equal to 54 km/h. What is the impulse imparted to the ball? (Mass of the ball is 0.15 kg.)
A stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are: [Choose the correct alternative]
| Lowest Point | Highest Point | |
| a) | mg – T1 | mg + T2 |
| b) | mg + T1 | mg – T2 |
| c) | `mg + T1 –(m_v_1^2)/R` | mg – T2 + (`mv_1^2`)/R |
| d) | `mg – T1 – (mv)/R` | mg + T2 + (mv_1^2)/R |
T1 and v1 denote the tension and speed at the lowest point. T2 and v2 denote corresponding values at the highest point.
An object is placed far away from all the objects that can exert force on it. A frame of reference is constructed by taking the origin and axes fixed in this object. Will the frame be necessarily inertial?
Two objects A and B are thrown upward simultaneously with the same speed. The mass of A is greater than that of B. Suppose the air exerts a constant and equal force of resistance on the two bodies.
If the tension in the cable supporting an elevator is equal to the weight of the elevator, the elevator may be
(a) going up with increasing speed
(b) going down with increasing speed
(c) going up with uniform speed
(d) going down with uniform speed
In a simple Atwood machine, two unequal masses m1 and m2 are connected by a string going over a clamped light smooth pulley. In a typical arrangement (In the following figure), m1 = 300 g and m2 = 600 g. The system is released from rest. (a) Find the distance travelled by the first block in the first two seconds; (b) find the tension in the string; (c) find the force exerted by the clamp on the pulley.
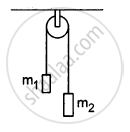
Consider the Atwood machine of the previous problem. The larger mass is stopped for a moment, 2.0 s after the system is set into motion. Find the time that elapses before the string is tight again.
In the following figure shows a uniform rod of length 30 cm and mass 3.0 kg. The strings shown in the figure are pulled by constant forces of 20 N and 32 N. Find the force exerted by the 20 cm part of the rod on the 10 cm part. All the surfaces are smooth and the strings and the pulleys are light.

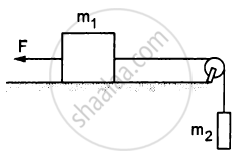
A constant force F = m2g/2 is applied on the block of mass m1 as shown in the following figure. The string and the pulley are light and the surface of the table is smooth. Find the acceleration of m1.
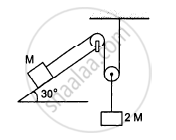
Find the acceleration of the block of mass M in the situation shown in the following figure. All the surfaces are frictionless and the pulleys and the string are light.
A block is kept on the floor of an elevator at rest. The elevator starts descending with an acceleration of 12 m/s2. Find the displacement of the block during the first 0.2 s after the start. Take g = 10 m/s2.
Two balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare:
(i) Their inertia.
(ii) Their momentum.
(iii) The force needed to stop them in the same time.
Write the mathematical form of Newton's second law of motion. State the conditions if any.
A body of mass 5 kg is moving with velocity 2 m s-1. Calculate its linear momentum.
An electron of mass 9 × 10−31 kg is moving with a linear velocity of 6 × 107 ms−1. Calculate the linear momentum of electron.
A body of mass 200 g is moving with a velocity of 5 ms−1. If the velocity of the body changes to 17 ms−1, calculate the change in linear momentum of the body.
A stone is dropped from a tower 98 m high. With what speed should a second stone be thrown 1 s later so that both hit the ground at the same time?
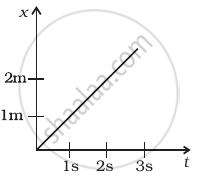
Figure shows (x, t), (y, t ) diagram of a particle moving in 2-dimensions.
|
|
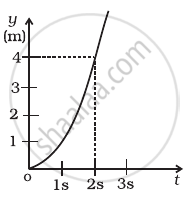 (b) |
If the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle.