Advertisements
Advertisements
Question
The monkey B, shown in the following figure, is holding on to the tail of monkey A that is climbing up a rope. The masses of monkeys A and B are 5 kg and 2 kg, respectively. If A can tolerate a tension of 30 N in its tail, what force should it apply on the rope in order to carry monkey B with it? Take g = 10 m/s2.
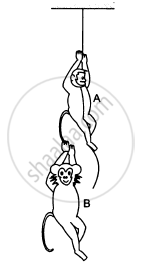
Solution
Let the acceleration of monkey A upwards be a, so that a maximum tension of 30 N is produced in its tail.
T − 5g − 30 − 5a = 0 ...(i)
30 − 2g − 2a = 0 ...(ii)
From equations (i) and (ii), we have:
T = 105 N (max.)
and a = 5 m/s2
So, A can apply a maximum force of 105 N on the rope to carry monkey B with it.
For minimum force, there is no acceleration of A and B.
T1 = weight of monkey B
⇒ T1 = 20 N
Rewriting equation (i) for monkey A, we get:
T − 5g − 20 = 0
⇒ T = 70 N
∴ To carry monkey B with it, monkey A should apply a force of magnitude between 70 N and 105 N.
APPEARS IN
RELATED QUESTIONS
The below figure shows the position-time graph of a particle of mass 4 kg.
- What is the force on the particle for t < 0, t > 4 s, 0 < t < 4 s?
- What is the impulse at t = 0 and t = 4 s? (Consider one-dimensional motion only.)

A helicopter of mass 1000 kg rises with a vertical acceleration of 15 m s–2. The crew and the passengers weigh 300 kg. Give the magnitude and direction of the
(a) force on the floor by the crew and passengers,
(b) action of the rotor of the helicopter on the surrounding air,
(c) force on the helicopter due to the surrounding air.
You are travelling in a car. The driver suddenly applies the brakes and you are pushed forward. Why does this happen?
An object is placed far away from all the objects that can exert force on it. A frame of reference is constructed by taking the origin and axes fixed in this object. Will the frame be necessarily inertial?
A particle of mass 0.3 kg is subjected to a force F = −kx with k = 15 N/m. What will be its initial acceleration if it is released from a point x = 20 cm?
An empty plastic box of mass m is found to accelerate up at the rate of g/6 when placed deep inside water. How much sand should be put inside the box so that it may accelerate down at the rate of g/6?
A monkey of mass 15 kg is climbing a rope fixed to a ceiling. If it wishes to go up with an acceleration of 1 m/s2, how much force should it apply on the rope? If the rope is 5 m long and the monkey starts from rest, how much time will it take to reach the ceiling?
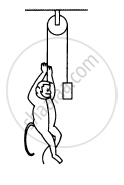
A monkey is climbing on a rope that goes over a smooth light pulley and supports a block of equal mass at the other end in the following figure. Show that whatever force the monkey exerts on the rope, the monkey and the block move in the same direction with equal acceleration. If initially both were at rest, their separation will not change as time passes.
Define linear momentum and state its S.I. unit.
Show that the rate of change of momentum = mass × acceleration. Under what condition does this relation hold?
Write the mathematical form of Newton's second law of motion. State the conditions if any.
Use Newton's second law of motion to explain the following instance :
A cricketer pulls his hands back while catching a fast moving cricket ball .
Use Newton's second law of motion to explain the following instance :
An athlete prefers to land on sand instead of hard floor while taking a high jump .
The correct form of Newton's second law is :
A ball is thrown vertically upwards. It returns 6 s later. Calculate : The greatest height reached by the ball . (Take g = 10 m s-2)
Define Newton’s second law of motion.
Name the physical entity used for quantifying the motion of a body.
Name the physical quantity which equals the rate of change of linear momentum.
A hockey player is moving northward and suddenly turns westward with the same speed to avoid an opponent. The force that acts on the player is ______.
A body of mass 2 kg travels according to the law x(t) = pt + qt2 + rt3 where p = 3 ms−1, q = 4 ms−2 and r = 5 ms−3. The force acting on the body at t = 2 seconds is ______.
