Advertisements
Advertisements
प्रश्न
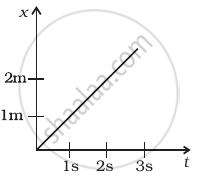
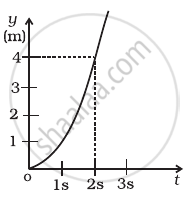
Figure shows (x, t), (y, t ) diagram of a particle moving in 2-dimensions.
|
|
 (b) |
If the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle.
उत्तर
Clearly, from the diagram (a), the variation can be related as x = t
⇒ `(dx)/(dt)` = 1 m/s
ax = 0
From diagram (b) y = t2
⇒ `(dy)/(dt)` = 2t or ay = `(d^2y)/(dt^2)` = 2 m/s2
Hence, Iy = may = 500 × 10–3 × 2 = 1 N .....(∵ m = 500 g)
Fx = max = 0
Hence, net force, F = `sqrt(F_x^2 + F_y^2)` = Fy = 1 N .....(along y-axis)
APPEARS IN
संबंधित प्रश्न
A spy jumps from an airplane with his parachute. The spy accelerates downward for some time when the parachute opens. The acceleration is suddenly checked and the spy slowly falls to the ground. Explain the action of the parachute in checking the acceleration.
If the tension in the cable supporting an elevator is equal to the weight of the elevator, the elevator may be
(a) going up with increasing speed
(b) going down with increasing speed
(c) going up with uniform speed
(d) going down with uniform speed
A small block B is placed on another block A of mass 5 kg and length 20 cm. Initially, the block B is near the right end of block A (In the following Figure). A constant horizontal force of 10 N is applied to the block A. All the surfaces are assumed frictionless. Find the time that elapses before block B separates from A.

A man has fallen into a ditch of width d and two of his friends are slowly pulling him out using a light rope and two fixed pulleys as shown in the following figure. Show that the force (assumed equal for both the friends) exerted by each friend on the road increases as the man moves up. Find the force when the man is at a depth h.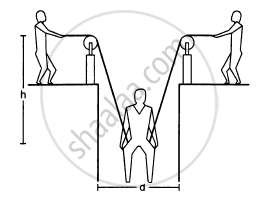
Find the reading of the spring balance shown in the following figure. The elevator is going up with an acceleration g/10, the pulley and the string are light and the pulley is smooth.

An empty plastic box of mass m is found to accelerate up at the rate of g/6 when placed deep inside water. How much sand should be put inside the box so that it may accelerate down at the rate of g/6?
Consider the Atwood machine of the previous problem. The larger mass is stopped for a moment, 2.0 s after the system is set into motion. Find the time that elapses before the string is tight again.
A pebble is thrown vertically upwards with a speed of 20 m s-1. How high will it be after 2 s? (Take g = 10 m s-2)
A stone is dropped freely from the top of a tower and it reaches the ground in 4 s. Taking g = 10m s-2, calculate the height of the tower.
What do you mean by an impulsive force?