Advertisements
Advertisements
Question
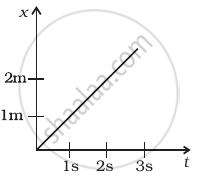
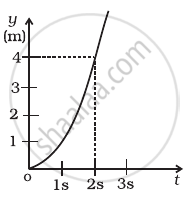
Figure shows (x, t), (y, t ) diagram of a particle moving in 2-dimensions.
|
|
 (b) |
If the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle.
Solution
Clearly, from the diagram (a), the variation can be related as x = t
⇒ `(dx)/(dt)` = 1 m/s
ax = 0
From diagram (b) y = t2
⇒ `(dy)/(dt)` = 2t or ay = `(d^2y)/(dt^2)` = 2 m/s2
Hence, Iy = may = 500 × 10–3 × 2 = 1 N .....(∵ m = 500 g)
Fx = max = 0
Hence, net force, F = `sqrt(F_x^2 + F_y^2)` = Fy = 1 N .....(along y-axis)
APPEARS IN
RELATED QUESTIONS
An aircraft executes a horizontal loop at a speed of 720 km/h with its wings banked at 15°. What is the radius of the loop?
A monkey of mass 40 kg climbs on a rope in given Figure which can stand a maximum tension of 600 N. In which of the following cases will the rope break: the monkey
(a) climbs up with an acceleration of 6 m s–2
(b) climbs down with an acceleration of 4 m s–2
(c) climbs up with a uniform speed of 5 m s–1
(d) falls down the rope nearly freely under gravity?
(Ignore the mass of the rope).

The rear side of a truck is open and a box of 40 kg mass is placed 5 m away from the open end as shown in Figure. The coefficient of friction between the box and the surface below it is 0.15. On a straight road, the truck starts from rest and accelerates with 2 m s–2. At what distance from the starting point does the box fall off the truck? (Ignore the size of the box).

Two objects A and B are thrown upward simultaneously with the same speed. The mass of A is greater than that of B. Suppose the air exerts a constant and equal force of resistance on the two bodies.
Two blocks of equal mass m are tied to each other through a light string. One of the blocks is pulled along the line joining them with a constant force F. Find the tension in the string joining the blocks.
Find the acceleration of the blocks A and B in the three situations shown in the following figure.

Show that the rate of change of momentum = mass × acceleration. Under what condition does this relation hold?
The linear momentum of a ball of mass 50 g is 0.5 kg m s-1. Find its velocity.
Why is it advantageous to turn before taking a long jump?
In the previous problem (5.3), the magnitude of the momentum transferred during the hit is ______.