Advertisements
Advertisements
प्रश्न
Find the acceleration of the block of mass M in the situation shown in the following figure. All the surfaces are frictionless and the pulleys and the string are light.
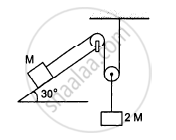
उत्तर
The free-body diagram of the system is shown below: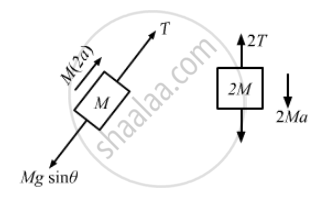
Let acceleration of the block of mass 2M be a.
So, acceleration of the block of mass M will be 2a.
M(2a) + Mgsinθ − T = 0
⇒ T = 2Ma + Mgsinθ ...(i)
2T + 2Ma − 2Mg = 0
From equation (i),
2(2Ma + Mgsinθ) + 2Ma − 2Mg = 0
4Ma + 2Mgsinθ + 2Ma − Mg = 0
6Ma + 2Mgsin30° + 2Mg = 0
6Ma = Mg
\[\Rightarrow a = \frac{g}{6}\]
Hence, the acceleration of mass
\[M = 2a = 2 \times \frac{g}{6} = \frac{g}{3} \left (\text{ up the plane }\right) .\]
APPEARS IN
संबंधित प्रश्न
A stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are: [Choose the correct alternative]
| Lowest Point | Highest Point | |
| a) | mg – T1 | mg + T2 |
| b) | mg + T1 | mg – T2 |
| c) | `mg + T1 –(m_v_1^2)/R` | mg – T2 + (`mv_1^2`)/R |
| d) | `mg – T1 – (mv)/R` | mg + T2 + (mv_1^2)/R |
T1 and v1 denote the tension and speed at the lowest point. T2 and v2 denote corresponding values at the highest point.
A block of mass 15 kg is placed on a long trolley. The coefficient of static friction between the block and the trolley is 0.18. The trolley accelerates from rest with 0.5 ms–2 for 20 s and then moves with uniform velocity. Discuss the motion of the block as viewed by (a) a stationary observer on the ground, (b) an observer moving with the trolley.
If the tension in the cable supporting an elevator is equal to the weight of the elevator, the elevator may be
(a) going up with increasing speed
(b) going down with increasing speed
(c) going up with uniform speed
(d) going down with uniform speed
A block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block by another string. Find the tensions in the two strings. Take g = 10 m/s2.
The force of buoyancy exerted by the atmosphere on a balloon is B in the upward direction and remains constant. The force of air resistance on the balloon acts opposite the direction of velocity and is proportional to it. The balloon carries a mass M and is found to fall to the earth's surface with a constant velocity v. How much mass should be removed from the balloon so that it may rise with a constant velocity v?
Consider the situation shown in the following figure All the surfaces are frictionless and the string and the pulley are light. Find the magnitude of acceleration of the two blocks.

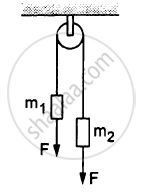
In the following figure, m1 = 5 kg, m2 = 2 kg and F = 1 N. Find the acceleration of either block. Describe the motion of m1 if the string breaks but F continues to act.
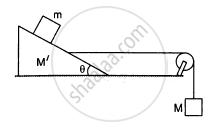
Find the mass M of the hanging block in the following figure that will prevent the smaller block from slipping over the triangular block. All the surfaces are frictionless and the strings and the pulleys are light.
State Newton's second law of motion. Under what condition does it take the form F = ma?
The correct form of Newton's second law is :
The unit of linear momentum is :
A pebble is dropped freely in a well from its top. It takes 20 s for the pebble to reach the water surface in the well. Taking g = 10 m s-2 and speed of sound = 330 m s-1. Find : The depth of water surface
State two factors which determine the momentum of a body.
Multiple Choice Question. Select the correct option.
Which of the following are vector quantities?
Name the physical quantity which equals the rate of change of linear momentum.
What do you mean by an impulsive force?
State Newton's second law of motion.
A body of mass 400 g is resting on a frictionless table. Find the acceleration of the body when acted upon by a force of 0.02 N.
A stone is dropped from a cliff 98 m high.
How long will it take to fall to the foot of the cliff?
A stone is dropped from a tower 98 m high. With what speed should a second stone be thrown 1 s later so that both hit the ground at the same time?
Why does a child feel more pain when she falls down on a hard cement floor, than when she falls on the soft muddy ground in the garden?
