Advertisements
Advertisements
Question
In a simple Atwood machine, two unequal masses m1 and m2 are connected by a string going over a clamped light smooth pulley. In a typical arrangement (In the following figure), m1 = 300 g and m2 = 600 g. The system is released from rest. (a) Find the distance travelled by the first block in the first two seconds; (b) find the tension in the string; (c) find the force exerted by the clamp on the pulley.
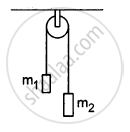
Solution
The masses of the blocks are m1 = 0.3 kg and m2 = 0.6 kg
The free-body diagrams of both the masses are shown below: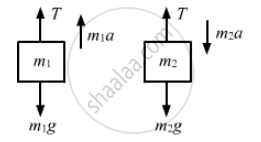
For mass m1,
T − m1g = m1a ...(i)
For mass m2,
m2g − T= m2a ...(ii)
Adding equations (i) and (ii), we get:
g(m2 − m1) = a(m1 + m2)
\[\Rightarrow a = g{\left( \frac{m_2 - m_1}{m_1 + m_2} \right)}$\]
\[ = 9 . 8 \times \frac{0 . 6 - 0 . 3}{0 . 6 + 0 . 3}\]
\[ = 3 . 266 m/ s^2\]
(a) t = 2 s, a = 3.266 ms−2, u = 0
So, the distance travelled by the body,
\[S = ut + \frac{1}{2}a t^2 \]
\[ = 0 + \frac{1}{2}\left( 3 . 266 \right) 2^2 = 6 . 5 m\]
(b) From equation (i),
T = m1 (g + a)
= 0.3 (9.8 + 3.26) = 3.9 N
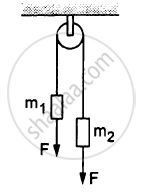
(c)The force exerted by the clamp on the pulley,
F = 2T = 2 × 3.9 = 7.8 N
APPEARS IN
RELATED QUESTIONS
A spy jumps from an airplane with his parachute. The spy accelerates downward for some time when the parachute opens. The acceleration is suddenly checked and the spy slowly falls to the ground. Explain the action of the parachute in checking the acceleration.
When a horse pulls a cart, the force that helps the horse to move forward is the force exerted by
A block of mass m is placed on a smooth wedge of inclination θ. The whole system is accelerated horizontally so that the block does not slip on the wedge. The force exerted by the wedge on the block has a magnitude.
In a TV picture tube, electrons are ejected from the cathode with negligible speed and they attain a velocity of 5 × 106 m/s in travelling one centimetre. Assuming straight-line motion, find the constant force exerted on the electrons. The mass of an electron is 9.1 × 10−31 kg.
Two blocks A and B of mass mA and mB , respectively, are kept in contact on a frictionless table. The experimenter pushes block A from behind, so that the blocks accelerate. If block A exerts force F on block B, what is the force exerted by the experimenter on block A?
The force of buoyancy exerted by the atmosphere on a balloon is B in the upward direction and remains constant. The force of air resistance on the balloon acts opposite the direction of velocity and is proportional to it. The balloon carries a mass M and is found to fall to the earth's surface with a constant velocity v. How much mass should be removed from the balloon so that it may rise with a constant velocity v?
A force \[\vec{F} = \vec{v} \times \vec{A}\] is exerted on a particle in addition to the force of gravity, where \[\vec{v}\] is the velocity of the particle and \[\vec{A}\] is a constant vector in the horizontal direction. With what minimum speed, a particle of mass m be projected so that it continues to move without being defelected and with a constant velocity?
In the following figure, m1 = 5 kg, m2 = 2 kg and F = 1 N. Find the acceleration of either block. Describe the motion of m1 if the string breaks but F continues to act.
A body of mass m moving with a velocity v is acted upon by a force. Write an expression for change in momentum in each of the following cases: (i) When v << c, (ii) When v → c and (iii) When v << c but m does not remain constant. Here, c is the speed of light.
Two balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare:
(i) Their inertia.
(ii) Their momentum.
(iii) The force needed to stop them in the same time.
State the Newton's second law of motion. What information do you get from it?
Use Newton's second law of motion to explain the following instance :
An athlete prefers to land on sand instead of hard floor while taking a high jump .
A force of 10 N acts on a body of mass 2 kg for 3 s, initially at rest. Calculate : Change in momentum of the body.
State the magnitude and direction of the force of gravity acting on the body of mass 5 kg. Take g = 9.8 m s-2.
A ball is thrown vertically upwards. It returns 6 s later. Calculate : The greatest height reached by the ball . (Take g = 10 m s-2)
An electron of mass 9 × 10−31 kg is moving with a linear velocity of 6 × 107 ms−1. Calculate the linear momentum of electron.
Prove mathematically F = ma
Multiple Choice Question. Select the correct option.
The impulse of a body is equal to:
What do you mean by linear momentum of a body? A force causes an acceleration of 10 ms-2 in a body of mass 1 kg. What acceleration will be caused by the same force in a body of mass 4 kg?
A stone is thrown vertically upward with a velocity of 9.8 m/s. When will it reach the ground?
