Advertisements
Advertisements
Question
The force of buoyancy exerted by the atmosphere on a balloon is B in the upward direction and remains constant. The force of air resistance on the balloon acts opposite the direction of velocity and is proportional to it. The balloon carries a mass M and is found to fall to the earth's surface with a constant velocity v. How much mass should be removed from the balloon so that it may rise with a constant velocity v?
Solution
Let M be mass of the balloon.
Let the air resistance force on balloon be F .
Given that F ∝ v.
⇒ F = kv,
where k = proportionality constant.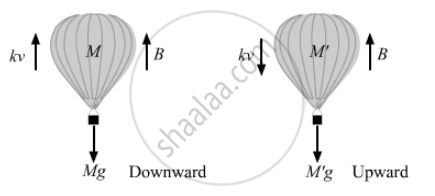
When the balloon is moving downward with constant velocity,
B + kv = Mg ...(i)
\[\Rightarrow M = \frac{B + kv}{g}\]
Let the mass of the balloon be M' so that it can rise with a constant velocity v in the upward direction.
B = Mg + kv
\[\Rightarrow M' = \frac{B + kv}{g}\]
∴ Amount of mass that should be removed = M − M'.
\[∆ M = \frac{B + kv}{g} - \frac{B - kv}{g}\]
\[ = \frac{B + kv - B + kv}{g}\]
\[ = \frac{2kv}{g} = \frac{2\left( Mg - B \right)}{g}\]
\[ = 2\left\{ M - \frac{B}{g} \right\}\]
APPEARS IN
RELATED QUESTIONS
A man of mass 70 kg stands on a weighing scale in a lift which is moving
- upwards with a uniform speed of 10 m s-1
- downwards with a uniform acceleration of 5 m s–2
- upwards with a uniform acceleration of 5 m s–2. What would be the readings on the scale in each case?
- What would be the reading if the lift mechanism failed and it hurtled down freely under gravity?
A batsman deflects a ball by an angle of 45° without changing its initial speed which is equal to 54 km/h. What is the impulse imparted to the ball? (Mass of the ball is 0.15 kg.)
A person drops a coin. Describe the path of the coin as seen by the person if he is in (a) a car moving at constant velocity and (b) in a free falling elevator.
Suppose you are running fast in a field and suddenly find a snake in front of you. You stop quickly. Which force is responsible for your deceleration?
A person says that he measured the acceleration of a particle to be non-zero even though no force was acting on the particle.
A small block B is placed on another block A of mass 5 kg and length 20 cm. Initially, the block B is near the right end of block A (In the following Figure). A constant horizontal force of 10 N is applied to the block A. All the surfaces are assumed frictionless. Find the time that elapses before block B separates from A.

An empty plastic box of mass m is found to accelerate up at the rate of g/6 when placed deep inside water. How much sand should be put inside the box so that it may accelerate down at the rate of g/6?
Consider the situation shown in the following figure. Both the pulleys and the string are light and all the surfaces are frictionless. (a) Find the acceleration of the mass M; (b) find the tension in the string; (c) calculate the force exerted by the clamp on the pulley A in the figure.
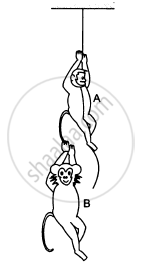
The monkey B, shown in the following figure, is holding on to the tail of monkey A that is climbing up a rope. The masses of monkeys A and B are 5 kg and 2 kg, respectively. If A can tolerate a tension of 30 N in its tail, what force should it apply on the rope in order to carry monkey B with it? Take g = 10 m/s2.
A block is kept on the floor of an elevator at rest. The elevator starts descending with an acceleration of 12 m/s2. Find the displacement of the block during the first 0.2 s after the start. Take g = 10 m/s2.
A body of mass m moving with a velocity v is acted upon by a force. Write an expression for change in momentum in each of the following cases: (i) When v << c, (ii) When v → c and (iii) When v << c but m does not remain constant. Here, c is the speed of light.
Use Newton's second law of motion to explain the following instance :
A cricketer pulls his hands back while catching a fast moving cricket ball .
The unit of linear momentum is :
A force acts for 10 s on a stationary body of mass 100 kg, after which the force ceases to act. The body moves through a distance of 100 m in the next 5 s. Calculate: The velocity acquired by the body.
A pebble is dropped freely in a well from its top. It takes 20 s for the pebble to reach the water surface in the well. Taking g = 10 m s-2 and speed of sound = 330 m s-1. Find : The time when echo is heard after the pebble is dropped.
Name the physical quantity which equals the rate of change of linear momentum.
State Newton's second law of motion. Is Newton's first law of motion contained in Newton's second law of motion?
What do you mean by the conservation of momentum? Briefly, explain the collision between two bodies and the conservation of momentum.
The INCORRECT statement about Newton's second law of motion is
A body of mass 2 kg travels according to the law x(t) = pt + qt2 + rt3 where p = 3 ms−1, q = 4 ms−2 and r = 5 ms−3. The force acting on the body at t = 2 seconds is ______.
