Advertisements
Advertisements
Question
A body of mass m moving with a velocity v is acted upon by a force. Write an expression for change in momentum in each of the following cases: (i) When v << c, (ii) When v → c and (iii) When v << c but m does not remain constant. Here, c is the speed of light.
Solution
(i) When v << c,
Δp = Δ(mv) = mΔv
(ii) When v → c,
Δp = Δ(mv)
(iii) When v<<c but m does not remain constant.
Δp = Δ(mv)
APPEARS IN
RELATED QUESTIONS
A rocket with a lift-off mass 20,000 kg is blasted upwards with an initial acceleration of 5.0 m s–2. Calculate the initial thrust (force) of the blast.
You are travelling in a car. The driver suddenly applies the brakes and you are pushed forward. Why does this happen?
A car accelerates on a horizontal road due to the force exerted by.
In the following figure shows a uniform rod of length 30 cm and mass 3.0 kg. The strings shown in the figure are pulled by constant forces of 20 N and 32 N. Find the force exerted by the 20 cm part of the rod on the 10 cm part. All the surfaces are smooth and the strings and the pulleys are light.

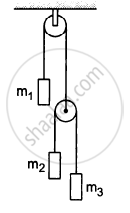
Let m1 = 1 kg, m2 = 2 kg and m3 = 3 kg in the following figure. Find the accelerations of m1, m2 and m3. The string from the upper pulley to m1 is 20 cm when the system is released from rest. How long will it take before m1 strikes the pulley?
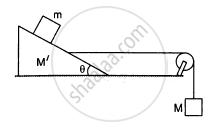
Find the mass M of the hanging block in the following figure that will prevent the smaller block from slipping over the triangular block. All the surfaces are frictionless and the strings and the pulleys are light.
A body of mass 200 g is moving with a velocity of 5 ms−1. If the velocity of the body changes to 17 ms−1, calculate the change in linear momentum of the body.
ame the law of motion which gives the definition of force.
Name the physical quantity which equals the rate of change of linear momentum.
Use Newton's second law to explain the following:
While catching a fast moving ball, we always pull our hands backwards.
