Advertisements
Advertisements
Question
A block of mass m is placed on a smooth wedge of inclination θ. The whole system is accelerated horizontally so that the block does not slip on the wedge. The force exerted by the wedge on the block has a magnitude.
Options
mg
mg/cosθ
mg cosθ
mg tanθ
Solution
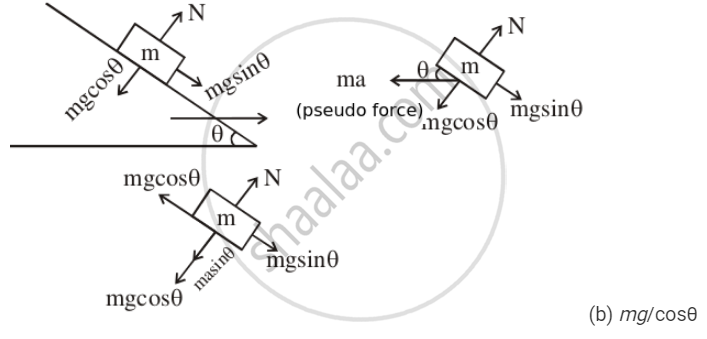
Free-body Diagram of the Small Block of Mass 'm'
The block is at equilibrium w.r.t. to wedge. Therefore,
mg sinθ = ma cosθ
⇒ a = gtanθ
Normal reaction on the block is
N = mg cosθ + ma sinθ
Putting the value of a, we get:
N = mg cosθ + mg tanθsinθ
\[N = mg\cos\theta + mg\frac{\sin\theta}{\cos\theta}\sin\ \theta N=\frac{mg}{\cos\theta}\]
APPEARS IN
RELATED QUESTIONS
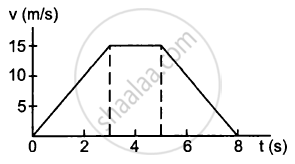
A particle of mass 50 g moves in a straight line. The variation of speed with time is shown in the following figure. Find the force acting on the particle at t = 2, 4 and 6 seconds.
A person is standing on a weighing machine placed on the floor of an elevator. The elevator starts going up with some acceleration, moves with uniform velocity for a while and finally decelerates to stop. The maximum and the minimum weights recorded are 72 kg and 60 kg, respectively. Assuming that the magnitudes of acceleration and deceleration are the same, find (a) the true weight of the person and (b) the magnitude of the acceleration. Take g = 9.9 m/s2.
Suppose the ceiling in the previous problem is that of an elevator which is going up with an acceleration of 2.0 m/s2. Find the elongation.
The force of buoyancy exerted by the atmosphere on a balloon is B in the upward direction and remains constant. The force of air resistance on the balloon acts opposite the direction of velocity and is proportional to it. The balloon carries a mass M and is found to fall to the earth's surface with a constant velocity v. How much mass should be removed from the balloon so that it may rise with a constant velocity v?
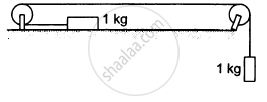
Calculate the tension in the string shown in the following figure. The pulley and the string are light and all the surfaces are frictionless. Take g = 10 m/s2.
A tennis ball and a cricket ball , both are stationary. To start motion in them .
Show that the rate of change of momentum = mass × acceleration. Under what condition does this relation hold?
Two bodies A and B of same mass are moving with velocities v and 2v, respectively. Compare their (i) inertia and (ii) momentum.
The linear momentum of a body of mass m moving with velocity v is :
The linear momentum of a ball of mass 50 g is 0.5 kg m s-1. Find its velocity.
A force of 10 N acts on a body of mass 2 kg for 3 s, initially at rest. Calculate : The velocity acquired by the body
State the magnitude and direction of the force of gravity acting on the body of mass 5 kg. Take g = 9.8 m s-2.
A ball is thrown vertically upwards. It returns 6 s later. Calculate : The greatest height reached by the ball . (Take g = 10 m s-2)
Calculate the velocity of a body of mass 0.5 kg, when it has a linear momentum of 5 Ns.
Which of the following has the largest inertia?
State Newton's second law of motion. Is Newton's first law of motion contained in Newton's second law of motion?
Use Newton's second law to explain the following:
While catching a fast moving ball, we always pull our hands backwards.
The INCORRECT statement about Newton's second law of motion is
A metre scale is moving with uniform velocity. This implies ______.
