Advertisements
Advertisements
प्रश्न
The rear side of a truck is open and a box of 40 kg mass is placed 5 m away from the open end as shown in Figure. The coefficient of friction between the box and the surface below it is 0.15. On a straight road, the truck starts from rest and accelerates with 2 m s–2. At what distance from the starting point does the box fall off the truck? (Ignore the size of the box).

उत्तर १
Force experienced by box, F = ma = 40 x 2 = 80 N
Frictional force `F_f = mu mg` = 0.15 x 40 x 10 = 60 N.
Backward acceleration produced in the box, `a =20/40("Net Force")/m`
`=>a = 0.5 "ms"^(-2)`
if t is time taken by the box to travel s =5 metre and fall off the truck, then from
`S = ut + 1/2 at^2`
`5 = 0 xx t + 1/2 xx 0.5 t^2`
`t= sqrt((5xx2)/0.5) = 4.47 s`
if the truck travel a distace x during this time, then again from
`S = ut + 1/2 at^2`
`x = 0 xx 4.47 + 1/2 xx 2(4.47)^2 = 19.98 m`
उत्तर २
Mass of the box, m = 40 kg
Coefficient of friction, μ = 0.15
Initial velocity, u = 0
Acceleration, a = 2 m/s2
Distance of the box from the end of the truck, s' = 5 m
As per Newton’s second law of motion, the force on the box caused by the accelerated motion of the truck is given by: F = ma
= 40 × 2 = 80 N
As per Newton’s third law of motion, a reaction force of 80 N is acting on the box in the backward direction. The backward motion of the box is opposed by the force of friction f, acting between the box and the floor of the truck. This force is given by:
f = μmg
= 0.15 × 40 × 10 = 60 N
∴Net force acting on the block:
Fnet = 80 – 60 = 20 N backward
The backward acceleration produced in the box is given by:
`a_"back" = F_"net"/m = 20/ 4 = 0.5 "m/s"^2`
Using the second equation of motion, time t can be calculated as:
`s' = ut + 1/2 a_"back" t^2`
`5 = 0 + 1/2 xx 0.5 xx t^2`
`:.t = sqrt20 s`
Hence, the box will fall from the truck after `sqrt20 s` from start
The distance s, travelled by the truck in `sqrt20 s` is given by the relation:
`s = ut + 1/2 at^2`
`=0 + 1/2xx2 xx(sqrt20)^2`
= 20 m
APPEARS IN
संबंधित प्रश्न
Suppose you are running fast in a field and suddenly find a snake in front of you. You stop quickly. Which force is responsible for your deceleration?
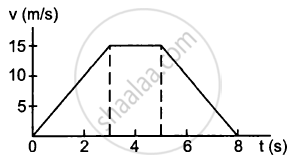
A particle of mass 50 g moves in a straight line. The variation of speed with time is shown in the following figure. Find the force acting on the particle at t = 2, 4 and 6 seconds.
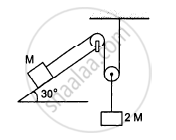
Consider the situation shown in the following figure. Both the pulleys and the string are light and all the surfaces are frictionless. (a) Find the acceleration of the mass M; (b) find the tension in the string; (c) calculate the force exerted by the clamp on the pulley A in the figure.
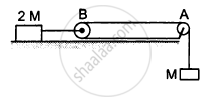
Find the acceleration of the block of mass M in the situation shown in the following figure. All the surfaces are frictionless and the pulleys and the string are light.
Show that the rate of change of momentum = mass × acceleration. Under what condition does this relation hold?
Use Newton's second law of motion to explain the following instance :
A cricketer pulls his hands back while catching a fast moving cricket ball .
The linear momentum of a ball of mass 50 g is 0.5 kg m s-1. Find its velocity.
A pebble is thrown vertically upwards with a speed of 20 m s-1. How high will it be after 2 s? (Take g = 10 m s-2)
The motion of a particle of mass m is given by x = 0 for t < 0 s, x(t) = A sin 4 pt for 0 < t < (1/4) s (A > o), and x = 0 for t > (1/4) s. Which of the following statements is true?
- The force at t = (1/8) s on the particle is – 16π2 Am.
- The particle is acted upon by on impulse of magnitude 4π2 A m at t = 0 s and t = (1/4) s.
- The particle is not acted upon by any force.
- The particle is not acted upon by a constant force.
- There is no impulse acting on the particle.
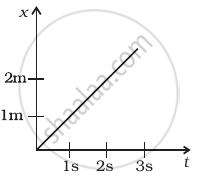
Figure shows (x, t), (y, t ) diagram of a particle moving in 2-dimensions.
|
|
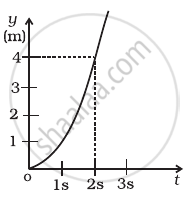 (b) |
If the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle.