Advertisements
Advertisements
प्रश्न
Show that the rate of change of momentum = mass × acceleration. Under what condition does this relation hold?
उत्तर १
Let a force 'F' be applied on a body of mass m for a time 't' due to which its velocity changes from u to v. Then,
Initial momentum of body = mu
Final momentum of body = mv
Change in momentum of the body in 't' seconds = mv - mu = m (v - u)
Rate of change of momentum = Change in momentum/time
= [m (v - u)]/t
However, acceleration a = Change in velocity/time = (v - u)/t
Therefore, rate of change of momentum = ma = mass × acceleration
This relation holds true when the mass of the body remains constant.
उत्तर २
According to newton second law
F = m X a
a= (v - u)/t.
F = m(v -u)/t
F = (mv - mu)/t
As F= m X a
ma = (mv - mu)/t
so rate of change of momentum = mass X acceleration.
This relation holds good when mass remains constant during motion.
संबंधित प्रश्न
A rocket with a lift-off mass 20,000 kg is blasted upwards with an initial acceleration of 5.0 m s–2. Calculate the initial thrust (force) of the blast.
Two bodies of masses 10 kg and 20 kg respectively kept on a smooth, horizontal surface are tied to the ends of a light string. A horizontal force F = 600 N is applied to
- A,
- B along the direction of string. What is the tension in the string in each case?
The figure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region
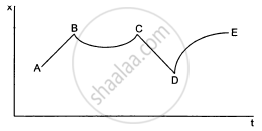
(a) AB
(b) BC
(c) CD
(d) DE
A force \[\vec{F} = \vec{v} \times \vec{A}\] is exerted on a particle in addition to the force of gravity, where \[\vec{v}\] is the velocity of the particle and \[\vec{A}\] is a constant vector in the horizontal direction. With what minimum speed, a particle of mass m be projected so that it continues to move without being defelected and with a constant velocity?
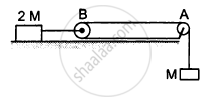
Consider the situation shown in the following figure. Both the pulleys and the string are light and all the surfaces are frictionless. (a) Find the acceleration of the mass M; (b) find the tension in the string; (c) calculate the force exerted by the clamp on the pulley A in the figure.
The correct form of Newton's second law is :
The linear momentum of a ball of mass 50 g is 0.5 kg m s-1. Find its velocity.
A force of 10 N acts on a body of mass 2 kg for 3 s, initially at rest. Calculate : The velocity acquired by the body
ame the law of motion which gives the definition of force.
State Newton's second law of motion.
A body of mass 400 g is resting on a frictionless table. Find the acceleration of the body when acted upon by a force of 0.02 N.
