Advertisements
Advertisements
प्रश्न
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
उत्तर
Let v be the speed of the car.
Since the motion is non-uniform, the acceleration has both radial (ar) and tangential (at) components.
\[\text{a}_\text{r} = \frac{\text{v}^2}{\text{R}}\]
\[ \text{a}_\text{t} = \frac{\text{dv}}{\text{dt}} = a\]
\[\text { Resultant magnitude } = \sqrt{\left( \frac{\text{v}^2}{R} \right)^2 + a^2}\]
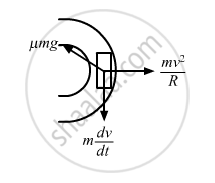
From free body diagram, we have :
\[\text{mN = m}\sqrt{\left( \frac{\text{v}^2}{R} \right)^2 + a^2}\]
\[ \Rightarrow \mu \text{ mg = m}\sqrt{\left( \frac{\text{v}^2}{R} \right)^2 + a^2}\]
\[ \Rightarrow \mu^2 g^2 = \frac{\text{v}^4}{R^2} + a^2\]
\[\Rightarrow \frac{\text{v}^4}{R^2} = ( \mu^2 g^2 - a^2 )\]
\[ \Rightarrow \text{v}^4 = ( \mu^2 g^2 - a^2 ) R^2 \]
\[ \Rightarrow \text{v} = [( \mu^2 g^2 - a^2 ) R^2 ]^{1/4}\]
APPEARS IN
संबंधित प्रश्न
A stone of mass 0.25 kg tied to the end of a string is whirled round in a circle of radius 1.5 m with a speed of 40 rev/min in a horizontal plane. What is the tension in the string? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
A disc revolves with a speed of `33 1/3` rev/min, and has a radius of 15 cm. Two coins are placed at 4 cm and 14 cm away from the centre of the record. If the co-efficient of friction between the coins and the record is 0.15, which of the coins will revolve with the record?
A 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
When a particle moves in a circle with a uniform speed
An object follows a curved path. The following quantities may remain constant during the motion
(a) speed
(b) velocity
(c) acceleration
(d) magnitude of acceleration.
A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
(a) The acceleration of the car is towards the centre of the path.
(b) The magnitude of the frictional force on the car is greater than \[\frac{\text{mv}^2}{\text{r}}\]
(c) The friction coefficient between the ground and the car is not less than a/g.
(d) The friction coefficient between the ground and the car is \[\mu = \tan^{- 1} \frac{\text{v}^2}{\text{rg}.}\]
The bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the string at this instant.
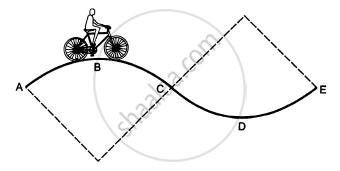
A track consists of two circular parts ABC and CDE of equal radius 100 m and joined smoothly as shown in figure. Each part subtends a right angle at its centre. A cycle weighing 100 kg together with the rider travels at a constant speed of 18 km/h on the track. (a) Find the normal contact force by the road on the cycle when it is at B and at D. (b) Find the force of friction exerted by the track on the tyres when the cycle is at B, C and. (c) Find the normal force between the road and the cycle just before and just after the cycle crosses C. (d) What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g = 10 m/s2.
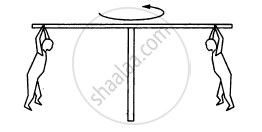
In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod (In the following figure). Let the mass of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
In a certain unit, the radius of gyration of a uniform disc about its central and transverse axis is `sqrt2.5`. Its radius of gyration about a tangent in its plane (in the same unit) must be ______.
Choose the correct option.
Consider the following cases:
(P) A planet revolving in an elliptical orbit.
(Q) A planet revolving in a circular orbit.
Principle of conservation of angular momentum comes in force in which of these?
A particle is moving in a radius R with constant speed v. The magnitude of average acceleration after half revolution is ____________.
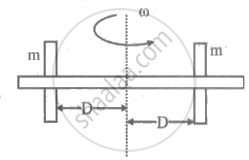
Two identical masses are connected to a horizontal thin (massless) rod as shown in the figure. When their distance from the pivot is D, a torque τ produces an angular acceleration of α1. The masses are now repositioned so that they are 2D from the pivot. The same torque produces an angular acceleration α2 which is given by ______
A child starts running from rest along a circular track of radius r with constant tangential acceleration a. After time the feels that slipping of shoes on the ground has started. The coefficient of friction between shoes and the ground is [g = acceleration due to gravity].
In negotiating curve on a flat road, a cyclist leans inwards by an angle e with the vertical in order to ______.
A racing car travels on a track (without banking) ABCDEFA (Figure). ABC is a circular arc of radius 2 R. CD and FA are straight paths of length R and DEF is a circular arc of radius R = 100 m. The co-efficient of friction on the road is µ = 0.1. The maximum speed of the car is 50 ms–1. Find the minimum time for completing one round.

Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
Find the angular acceleration of a particle in circular motion which slows down from 300 r.p.m. to 0 r.p.m. in 20 s.
Define centripetal force.
