Advertisements
Advertisements
Question
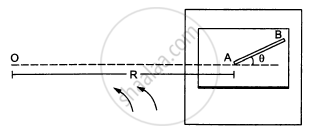
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular path of radius R (In the following figure). A smooth groove AB of length L(<<R) is made the surface of the table. The groove makes an angle θ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move at the point A in the groove and is released to move along AB. Find the time taken by the particle to reach the point B.
Solution
Let the mass of the particle be m.
Radius of the path = R
Angular velocity = ω
Force experienced by the particle = mω2R
The component of force mRω2 along the line AB (making an angle with the radius) provides the necessary force to the particle to move along AB.
\[\therefore m \omega^2 R \cos\theta = ma\]
\[ \Rightarrow a = \omega^2 R\cos\theta\]
Let the time taken by the particle to reach the point B be t.
\[\text { On using equation of motion, we get : }\]
\[L = ut + \frac{1}{2}a t^2 \]
\[ \Rightarrow L = \frac{1}{2} \omega^2 R\cos\theta t^2 \]
\[ \Rightarrow t^2 = \frac{2L}{\omega^2 R\cos\theta}\]
\[ \Rightarrow t = \sqrt{\frac{2L}{\omega^2 R\cos\theta}}\]
APPEARS IN
RELATED QUESTIONS
A disc revolves with a speed of `33 1/3` rev/min, and has a radius of 15 cm. Two coins are placed at 4 cm and 14 cm away from the centre of the record. If the co-efficient of friction between the coins and the record is 0.15, which of the coins will revolve with the record?
A smooth block loosely fits in a circular tube placed on a horizontal surface. The block moves in a uniform circular motion along the tube. Which wall (inner or outer) will exert a nonzero normal contact force on the block?
When a particle moves in a circle with a uniform speed
Water in a bucket is whirled in a vertical circle with string attached to it. The water does no fall down even when the bucket is inverted at the top of its path. We conclude that in this position
A stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
A coin placed on a rotating turntable just slips. If it is placed at a distance of 4 cm from the centre. If the angular velocity of the turntable is doubled, it will just slip at a distance of
A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it
A simple pendulum having a bob of mass m is suspended from the ceiling of a car used in a stunt film shooting. the car moves up along an inclined cliff at a speed v and makes a jump to leave the cliff and lands at some distance. Let R be the maximum height of the car from the top of the cliff. The tension in the string when the car is in air is
A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
(a) The acceleration of the car is towards the centre of the path.
(b) The magnitude of the frictional force on the car is greater than \[\frac{\text{mv}^2}{\text{r}}\]
(c) The friction coefficient between the ground and the car is not less than a/g.
(d) The friction coefficient between the ground and the car is \[\mu = \tan^{- 1} \frac{\text{v}^2}{\text{rg}.}\]
A stone is fastened to one end of a string and is whirled in a vertical circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
A simple pendulum is suspended from the ceiling of a car taking a turn of radius 10 m at a speed of 36 km/h. Find the angle made by he string of the pendulum with the vertical if this angle does not change during the turn. Take g = 10 m/s2.
The bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the string at this instant.
A block of mass m moves on a horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v writes
(a) the normal force by the wall on the block,
(b) the frictional force by a wall, and
(c) the tangential acceleration of the block.
(d) Integrate the tangential acceleration \[\left( \frac{dv}{dt} = v\frac{dv}{ds} \right)\] to obtain the speed of the block after one revolution.
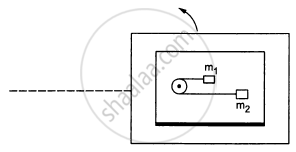
A table with smooth horizontal surface is placed in a circle of a large radius R (In the following figure). A smooth pulley of small radius is fastened to the table. Two masses m and 2m placed on the table are connected through a string going over the pulley. Initially the masses are held by a person with the string along the outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the masses as seen from the cabin and the tension in the string.
When seen from below, the blades of a ceiling fan are seen to be revolving anticlockwise and their speed is decreasing. Select the correct statement about the directions of its angular velocity and angular acceleration.
A body slides down a smooth inclined plane having angle θ and reaches the bottom with velocity v. If a body is a sphere, then its linear velocity at the bottom of the plane is
A wheel is subjected to uniform angular acceleration about its axis. The wheel is starting from rest and it rotates through an angle θ1, in first two seconds. In the next two seconds, it rotates through an angle θ2. The ratio θ1/θ2 is ____________.
A rigid body is rotating with angular velocity 'ω' about an axis of rotation. Let 'v' be the linear velocity of particle which is at perpendicular distance 'r' from the axis of rotation. Then the relation 'v = rω' implies that ______.
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2 then its resultant accelaration will be ______.
