Advertisements
Advertisements
Question
A simple pendulum is suspended from the ceiling of a car taking a turn of radius 10 m at a speed of 36 km/h. Find the angle made by he string of the pendulum with the vertical if this angle does not change during the turn. Take g = 10 m/s2.
Solution
Speed of the car = v = 36 km/hr = 10 m/s
Acceleration due to gravity = g = 10 m/s2
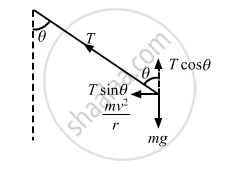
Let T be the tension in the string when the pendulum makes an angle θ with the vertical.
From the figure, we get :
\[\text{T}\sin\theta = \frac{\text{mv}^2}{r} . . . (\text{i})\]
\[T\cos\theta = \text{mg . . . (ii)}\]
\[ \Rightarrow \frac{\sin\theta}{\cos\theta} = \frac{\text{mv}^2}{\text{rmg}}\]
\[ \Rightarrow \tan\theta = \frac{\text{v}^2}{\text{rg}}\]
\[ \Rightarrow \theta = \tan^{- 1} \left( \frac{\text{v}^2}{\text{rg}} \right)\]
\[ = \tan^{- 1} \left[ \frac{100}{(10 \times 10)} \right]\]
\[ = \tan^{- 1} (1)\]
\[ \Rightarrow \theta= 45^\circ\]
APPEARS IN
RELATED QUESTIONS
A disc revolves with a speed of `33 1/3` rev/min, and has a radius of 15 cm. Two coins are placed at 4 cm and 14 cm away from the centre of the record. If the co-efficient of friction between the coins and the record is 0.15, which of the coins will revolve with the record?
A 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
A simple pendulum having a bob of mass m is suspended from the ceiling of a car used in a stunt film shooting. the car moves up along an inclined cliff at a speed v and makes a jump to leave the cliff and lands at some distance. Let R be the maximum height of the car from the top of the cliff. The tension in the string when the car is in air is
A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
(a) The acceleration of the car is towards the centre of the path.
(b) The magnitude of the frictional force on the car is greater than \[\frac{\text{mv}^2}{\text{r}}\]
(c) The friction coefficient between the ground and the car is not less than a/g.
(d) The friction coefficient between the ground and the car is \[\mu = \tan^{- 1} \frac{\text{v}^2}{\text{rg}.}\]
Find the acceleration of the moon with respect to the earth from the following data:
Distance between the earth and the moon = 3.85 × 105 km and the time taken by the moon to complete one revolution around the earth = 27.3 days.
Find the acceleration of a particle placed on the surface of the earth at the equator due to earth's rotation. The diameter of earth = 12800 km and it takes 24 hours for the earth to complete one revolution about its axis.
A stone is fastened to one end of a string and is whirled in a vertical circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
Suppose the bob of the previous problem has a speed of 1.4 m/s when the string makes an angle of 0.20 radian with the vertical. Find the tension at this instant. You can use cos θ ≈ 1 − θ2/2 and SINθ ≈ θ for small θ.
A motorcycle has to move with a constant speed on an over bridge which is in the form of a circular arc of radius R and has a total length L. Suppose the motorcycle starts from the highest point.(a) What can its maximum velocity be for which the contact with the road is not broken at the highest point? (b) If the motorcycle goes at speed 1/√2 times the maximum found in part (a), where will it lose the contact with the road? (c) What maximum uniform speed can it maintain on the bridge if it does not lose contact anywhere on the bridge?
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
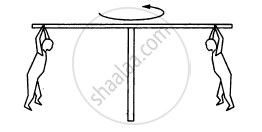
In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod (In the following figure). Let the mass of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
When seen from below, the blades of a ceiling fan are seen to be revolving anticlockwise and their speed is decreasing. Select the correct statement about the directions of its angular velocity and angular acceleration.
A particle is moving in a radius R with constant speed v. The magnitude of average acceleration after half revolution is ____________.
A child starts running from rest along a circular track of radius r with constant tangential acceleration a. After time the feels that slipping of shoes on the ground has started. The coefficient of friction between shoes and the ground is [g = acceleration due to gravity].
The escape velocity of a body from any planet, whose mass is six times the mass of earth and radius is twice the radius of earth will be
(v8 = escape velocity of a body from the earth's surface).
The centripetal force of a body moving in a circular path, if speed is made half and radius is made four times the original value, will ____________.
A rigid body is rotating with angular velocity 'ω' about an axis of rotation. Let 'v' be the linear velocity of particle which is at perpendicular distance 'r' from the axis of rotation. Then the relation 'v = rω' implies that ______.
If a cyclist doubles his speed while negotiating a curve, how does the tendency to overturn vary?
In negotiating curve on a flat road, a cyclist leans inwards by an angle e with the vertical in order to ______.
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
