Advertisements
Advertisements
Question
Find the acceleration of a particle placed on the surface of the earth at the equator due to earth's rotation. The diameter of earth = 12800 km and it takes 24 hours for the earth to complete one revolution about its axis.
Solution
Diameter of the Earth = 12800 km
So, radius of the Earth, R = 6400 km = 6.4 × 106 m
Time period of revolution of the Earth about its axis :
\[T = 24 \text{hr} = 24 \times 3600 \text{s}\]
\[\text{v} = \frac{2\pi r}{T}=\frac{2 \times 3 . 14 \times 64 \times {10}^6}{24 \times 3600}\]
\[\Rightarrow \text{v} = 465 . 185 \text{ m/s}\]
\[\text { Acceleration of the particle }: \]
\[a = \frac{v^2}{R} = \frac{\left( 465 . 185 \right)^2}{64 \times {10}^5} = 0 . 038 \text{ m/ s}^2\]
APPEARS IN
RELATED QUESTIONS
A stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
A train A runs from east to west and another train B of the same mass runs from west to east at the same speed along the equator. A presses the track with a force F1 and B presses the track with a force F2.
If the earth stop rotating, the apparent value of g on its surface will
A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
A simple pendulum having a bob of mass m is suspended from the ceiling of a car used in a stunt film shooting. the car moves up along an inclined cliff at a speed v and makes a jump to leave the cliff and lands at some distance. Let R be the maximum height of the car from the top of the cliff. The tension in the string when the car is in air is
Let θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension is the string is mg cos θ
A particle is going in a spiral path as shown in figure with constant speed.
Find the acceleration of the moon with respect to the earth from the following data:
Distance between the earth and the moon = 3.85 × 105 km and the time taken by the moon to complete one revolution around the earth = 27.3 days.
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
A hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical. A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is μ. Find the range of the angular speed for which the block will not slip.
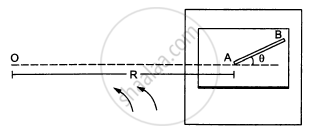
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular path of radius R (In the following figure). A smooth groove AB of length L(<<R) is made the surface of the table. The groove makes an angle θ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move at the point A in the groove and is released to move along AB. Find the time taken by the particle to reach the point B.
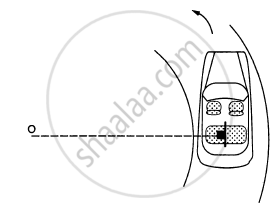
A car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road (In the following figure). A small block of mass 100 g is kept on the seat which rests against the plate. the friction coefficient between the block and the plate is. (a) Find the normal contact force exerted by the plate on the block. (b) The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
In a certain unit, the radius of gyration of a uniform disc about its central and transverse axis is `sqrt2.5`. Its radius of gyration about a tangent in its plane (in the same unit) must be ______.
In non-uniform circular motion, the ratio of tangential to radial acceleration is (r = radius, a = angular acceleration and v = linear velocity)
A child starts running from rest along a circular track of radius r with constant tangential acceleration a. After time the feels that slipping of shoes on the ground has started. The coefficient of friction between shoes and the ground is [g = acceleration due to gravity].
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2, then its resultant acceleration will be ______.
The real force 'F' acting on a particle of mass ' m' performing circular motion acts along the radius of circle 'r' and is directed towards the centre of circle. The square root of the magnitude of such force is (T = periodic time).
An engine is moving on a c1rcular path of radius 200 m with speed of 15 m/s. What will be the frequency heard by an observer who is at rest at the centre of the circular path, when engine blows the whistle with frequency 250 Hz?
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
Find the angular acceleration of a particle in circular motion which slows down from 300 r.p.m. to 0 r.p.m. in 20 s.
