Advertisements
Advertisements
Question
When seen from below, the blades of a ceiling fan are seen to be revolving anticlockwise and their speed is decreasing. Select the correct statement about the directions of its angular velocity and angular acceleration.
Options
Angular velocity upwards, angular acceleration downwards.
Angular velocity downwards, angular acceleration upwards.
Both, angular velocity and angular acceleration, upwards.
Both, angular velocity and angular acceleration, downwards.
Solution
Angular velocity downwards, angular acceleration upwards.
Explanation:
As seen below, the fan is rotating in the anticlockwise direction; therefore, by the right-hand thumb rule, the direction of the angular velocity vector is towards the observer. Therefore, the angular velocity vector points downward.
The speed of rotation of the fan decreases in the anticlockwise direction; therefore, the angular acceleration is in the opposite direction. Therefore, the angular acceleration vector points upwards.
APPEARS IN
RELATED QUESTIONS
A thin circular loop of radius R rotates about its vertical diameter with an angular frequency ω. Show that a small bead on the wire loop remains at its lowermost point for `omega <= sqrt(g/R)` .What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for `omega = sqrt("2g"/R)` ?Neglect friction.
A particle is kept fixed on a turntable rotating uniformly. As seen from the ground the particle goes in a circle, its speed is 20 cm/s and acceleration is 20 cm/s2. The particle is now shifted to a new position to make the radius half of the original value. The new value of the speed and acceleration will be
A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it
Three identical cars A, B and C are moving at the same speed on three bridges. The car A goes on a place bridge, B on a bridge convex upward and C goes on a bridge concave upward. Let FA, FB and FC be the normal forces exerted by the car on the bridges when they are at the middle of bridges.
If the earth stop rotating, the apparent value of g on its surface will
A simple pendulum having a bob of mass m is suspended from the ceiling of a car used in a stunt film shooting. the car moves up along an inclined cliff at a speed v and makes a jump to leave the cliff and lands at some distance. Let R be the maximum height of the car from the top of the cliff. The tension in the string when the car is in air is
A particle moves in a circle of radius 1.0 cm at a speed given by v = 2.0 t where v is cm/s and t in seconds.
(a) Find the radial acceleration of the particle at t = 1 s.
(b) Find the tangential acceleration at t = 1 s.
(c) Find the magnitude of the acceleration at t = 1 s.
Suppose the bob of the previous problem has a speed of 1.4 m/s when the string makes an angle of 0.20 radian with the vertical. Find the tension at this instant. You can use cos θ ≈ 1 − θ2/2 and SINθ ≈ θ for small θ.
Suppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
A turn of radius 20 m is banked for the vehicles going at a speed of 36 km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
A block of mass m is kept on a horizontal ruler. The friction coefficient between the ruler and the block is μ. The ruler is fixed at one end and the block is at a distance L from the fixed end. The ruler is rotated about the fixed end in the horizontal plane through the fixed end. (a) What can the maximum angular speed be for which the block does not slip? (b) If the angular speed of the ruler is uniformly increased from zero at an angular acceleration α, at what angular speed will the block slip?
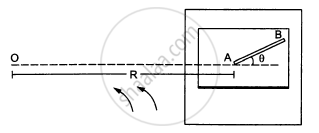
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular path of radius R (In the following figure). A smooth groove AB of length L(<<R) is made the surface of the table. The groove makes an angle θ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move at the point A in the groove and is released to move along AB. Find the time taken by the particle to reach the point B.
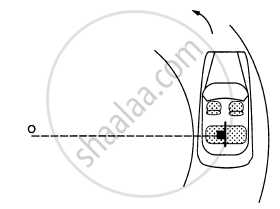
A car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road (In the following figure). A small block of mass 100 g is kept on the seat which rests against the plate. the friction coefficient between the block and the plate is. (a) Find the normal contact force exerted by the plate on the block. (b) The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
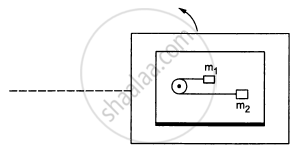
A table with smooth horizontal surface is placed in a circle of a large radius R (In the following figure). A smooth pulley of small radius is fastened to the table. Two masses m and 2m placed on the table are connected through a string going over the pulley. Initially the masses are held by a person with the string along the outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the masses as seen from the cabin and the tension in the string.
A particle of mass 1 kg, tied to a 1.2 m long string is whirled to perform the vertical circular motion, under gravity. The minimum speed of a particle is 5 m/s. Consider the following statements.
P) Maximum speed must be `5sqrt5` m/s.
Q) Difference between maximum and minimum tensions along the string is 60 N.
Select the correct option.
In a certain unit, the radius of gyration of a uniform disc about its central and transverse axis is `sqrt2.5`. Its radius of gyration about a tangent in its plane (in the same unit) must be ______.
A wheel is subjected to uniform angular acceleration about its axis. The wheel is starting from rest and it rotates through an angle θ1, in first two seconds. In the next two seconds, it rotates through an angle θ2. The ratio θ1/θ2 is ____________.
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2, then its resultant acceleration will be ______.
The real force 'F' acting on a particle of mass ' m' performing circular motion acts along the radius of circle 'r' and is directed towards the centre of circle. The square root of the magnitude of such force is (T = periodic time).
A rigid body is rotating with angular velocity 'ω' about an axis of rotation. Let 'v' be the linear velocity of particle which is at perpendicular distance 'r' from the axis of rotation. Then the relation 'v = rω' implies that ______.
An engine requires 5 seconds to go from a speed of 600 r.p.m. to 1200 r.p.m. How many revolutions does it make in this period?
A particle performs uniform circular motion in a horizontal plane. The radius of the circle is 10 cm. If the centripetal force F is kept constant but the angular velocity is halved, the new radius of the path will be ______.
In negotiating curve on a flat road, a cyclist leans inwards by an angle e with the vertical in order to ______.
An engine is moving on a c1rcular path of radius 200 m with speed of 15 m/s. What will be the frequency heard by an observer who is at rest at the centre of the circular path, when engine blows the whistle with frequency 250 Hz?
When a body slides down from rest along a smooth inclined plane making an angle of 45° with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the co-efficient of friction between the body and the rough plane.
A block of 200 g mass moves with a uniform speed in a horizontal circular groove, with vertical side walls of radius 20 cm. If the block takes 40 s to complete one round, the normal force by the side walls of the groove is ______.
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
