Advertisements
Advertisements
प्रश्न
Find the acceleration of the moon with respect to the earth from the following data:
Distance between the earth and the moon = 3.85 × 105 km and the time taken by the moon to complete one revolution around the earth = 27.3 days.
उत्तर
Distance between the Earth and the Moon:
r = 3.85 × 105 km = 3.85 × 108 m
Time taken by the Moon to revolve around the Earth:
T = 27.3 days
= 24 × 3600 × 27.3 s
= 2.36 × 106 s
Velocity of the Moon:
`v = (2pir)/T`
= `(2 × 3.14 × 3.85 xx 10^8)/(2.36 × 10^6)`
= 1025.41 m/s
Acceleration of the Moon:
`a = v^2/r`
= `(1025.42)^2/(3.85 xx 10^8)`
= 0.00275 m/s2
⇒ a = 2.73 × 10−3 m/s2
APPEARS IN
संबंधित प्रश्न
A disc revolves with a speed of `33 1/3` rev/min, and has a radius of 15 cm. Two coins are placed at 4 cm and 14 cm away from the centre of the record. If the co-efficient of friction between the coins and the record is 0.15, which of the coins will revolve with the record?
A 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
A car moves at a constant speed on a road as shown in figure. The normal force by the road on the car NA and NB when it is at the points A and B respectively.

Water in a bucket is whirled in a vertical circle with string attached to it. The water does no fall down even when the bucket is inverted at the top of its path. We conclude that in this position
A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
An object follows a curved path. The following quantities may remain constant during the motion
(a) speed
(b) velocity
(c) acceleration
(d) magnitude of acceleration.
Assume that the earth goes round the sun in a circular orbit with a constant speed of 30 kms
A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
(a) The acceleration of the car is towards the centre of the path.
(b) The magnitude of the frictional force on the car is greater than \[\frac{\text{mv}^2}{\text{r}}\]
(c) The friction coefficient between the ground and the car is not less than a/g.
(d) The friction coefficient between the ground and the car is \[\mu = \tan^{- 1} \frac{\text{v}^2}{\text{rg}.}\]
A block of mass m is kept on a horizontal ruler. The friction coefficient between the ruler and the block is μ. The ruler is fixed at one end and the block is at a distance L from the fixed end. The ruler is rotated about the fixed end in the horizontal plane through the fixed end. (a) What can the maximum angular speed be for which the block does not slip? (b) If the angular speed of the ruler is uniformly increased from zero at an angular acceleration α, at what angular speed will the block slip?
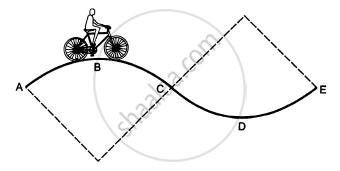
A track consists of two circular parts ABC and CDE of equal radius 100 m and joined smoothly as shown in figure. Each part subtends a right angle at its centre. A cycle weighing 100 kg together with the rider travels at a constant speed of 18 km/h on the track. (a) Find the normal contact force by the road on the cycle when it is at B and at D. (b) Find the force of friction exerted by the track on the tyres when the cycle is at B, C and. (c) Find the normal force between the road and the cycle just before and just after the cycle crosses C. (d) What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g = 10 m/s2.
A particle is projected with a speed u at an angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circular circle? This radius is called the radius of curvature of the curve at the point.
What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes an angle θ/2 with the horizontal?
A rope is wound around a solid cylinder of mass 1 kg and radius 0.4 m. What is the angular acceleration of cylinder, if the rope is pulled with a force of 25 N? (Cylinder is rotating about its own axis.)
Angular displacement (θ) of a flywheel varies with time as θ = at + bt2 + ct3 then angular acceleration is given by ____________.
If a cyclist doubles his speed while negotiating a curve, how does the tendency to overturn vary?
An engine requires 5 seconds to go from a speed of 600 r.p.m. to 1200 r.p.m. How many revolutions does it make in this period?
An engine is moving on a c1rcular path of radius 200 m with speed of 15 m/s. What will be the frequency heard by an observer who is at rest at the centre of the circular path, when engine blows the whistle with frequency 250 Hz?
When a body slides down from rest along a smooth inclined plane making an angle of 45° with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the co-efficient of friction between the body and the rough plane.
Define centripetal force.
