Advertisements
Advertisements
प्रश्न
A person stands on a spring balance at the equator. By what fraction is the balance reading less than his true weight?
उत्तर
Balance reading = Normal force on the balance by the Earth.
At equator, the normal force (N) on the spring balance :
N = mg − mω2r
True weight = mg
Therefore, we have :
\[\text { Fraction less than the true weight } = \frac{\text{mg - (mg - m }\omega^2 r)}{\text{mg}}\]
\[ = \frac{\omega^2 r}{g} = \left( \frac{2\pi}{24 \times 3600} \right)^2 \left( \frac{6 . 4 \times {10}^6}{10} \right)\]
\[= 3 . 5 \times {10}^{- 3}\]
APPEARS IN
संबंधित प्रश्न
A stone of mass 0.25 kg tied to the end of a string is whirled round in a circle of radius 1.5 m with a speed of 40 rev/min in a horizontal plane. What is the tension in the string? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
A 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
Water in a bucket is whirled in a vertical circle with string attached to it. The water does no fall down even when the bucket is inverted at the top of its path. We conclude that in this position
A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it
A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
(a) velocity remains constant
(b) speed remains constant
(c) acceleration remains constant
(d) tangential acceleration remains constant.
A motorcycle has to move with a constant speed on an over bridge which is in the form of a circular arc of radius R and has a total length L. Suppose the motorcycle starts from the highest point.(a) What can its maximum velocity be for which the contact with the road is not broken at the highest point? (b) If the motorcycle goes at speed 1/√2 times the maximum found in part (a), where will it lose the contact with the road? (c) What maximum uniform speed can it maintain on the bridge if it does not lose contact anywhere on the bridge?
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
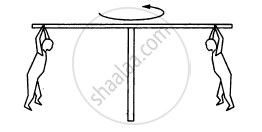
In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod (In the following figure). Let the mass of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
A particle is projected with a speed u at an angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circular circle? This radius is called the radius of curvature of the curve at the point.
What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes an angle θ/2 with the horizontal?
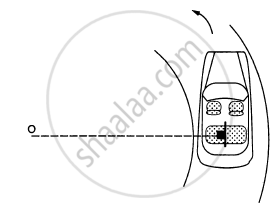
A car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road (In the following figure). A small block of mass 100 g is kept on the seat which rests against the plate. the friction coefficient between the block and the plate is. (a) Find the normal contact force exerted by the plate on the block. (b) The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
In non-uniform circular motion, the ratio of tangential to radial acceleration is (r = radius, a = angular acceleration and v = linear velocity)
A particle of mass m is performing UCM along a circle of radius r. The relation between centripetal acceleration a and kinetic energy E is given by
A particle is moving in a radius R with constant speed v. The magnitude of average acceleration after half revolution is ____________.
The escape velocity of a body from any planet, whose mass is six times the mass of earth and radius is twice the radius of earth will be
(v8 = escape velocity of a body from the earth's surface).
A rope is wound around a solid cylinder of mass 1 kg and radius 0.4 m. What is the angular acceleration of cylinder, if the rope is pulled with a force of 25 N? (Cylinder is rotating about its own axis.)
An engine requires 5 seconds to go from a speed of 600 r.p.m. to 1200 r.p.m. How many revolutions does it make in this period?
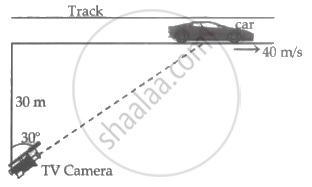
A racing car is travelling along a track at a constant speed of 40 m/s. A T.V. cameraman is recording the event from a distance of 30 m directly away from the track as shown in the figure. In order to keep the car under view in the position shown, the angular speed with which the camera should be rotated is ______.
Define centripetal force.
