Advertisements
Advertisements
प्रश्न
A car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road (In the following figure). A small block of mass 100 g is kept on the seat which rests against the plate. the friction coefficient between the block and the plate is. (a) Find the normal contact force exerted by the plate on the block. (b) The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
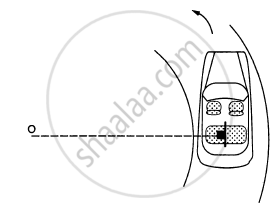
उत्तर
Given :
Speed of the car = v = 36 km/h = 10 m/s
Radius of the road = r = 50 m
Friction coefficient between the block and the plate = μ = 0.58
Mass of the small body = m = 100 g = 0.1 kg
(a) Let us find the normal contact force (N) exerted by the plant of the block.
\[N = \frac{\text{mv}^2}{r} = 0 . 1 \times \frac{100}{50} = \frac{1}{5} = 0 . 2\]
(b) The plate is turned; so, the angle between the normal to the plate and the radius of the rod slowly increases.
Therefore, we have :
\[N = \frac{\text{mv}^2}{r}\text{ cos }\theta . . . \left(\text{ i }\right)\]
\[\mu N = \frac{m v^2}{r}\text{ sin }\theta . . . \](ii)
\[\text { On using i and ii , we get : } \]
\[\frac{\mu m v^2}{r}\cos\theta = \frac{\text{mv}^2}{r}\sin\theta\]
\[ \Rightarrow \mu = \text{ tan }\theta\]
\[ \Rightarrow \theta = \tan^{- 1} (0 . 58) \approx 30^\circ\]
APPEARS IN
संबंधित प्रश्न
You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘death-well’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m?
A car moves at a constant speed on a road as shown in figure. The normal force by the road on the car NA and NB when it is at the points A and B respectively.

A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
A particle is going in a spiral path as shown in figure with constant speed.
Find the acceleration of the moon with respect to the earth from the following data:
Distance between the earth and the moon = 3.85 × 105 km and the time taken by the moon to complete one revolution around the earth = 27.3 days.
Find the acceleration of a particle placed on the surface of the earth at the equator due to earth's rotation. The diameter of earth = 12800 km and it takes 24 hours for the earth to complete one revolution about its axis.
A particle moves in a circle of radius 1.0 cm at a speed given by v = 2.0 t where v is cm/s and t in seconds.
(a) Find the radial acceleration of the particle at t = 1 s.
(b) Find the tangential acceleration at t = 1 s.
(c) Find the magnitude of the acceleration at t = 1 s.
A scooter weighing 150 kg together with its rider moving at 36 km/hr is to take a turn of a radius 30 m. What horizontal force on the scooter is needed to make the turn possible ?
The bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the string at this instant.
A person stands on a spring balance at the equator. By what fraction is the balance reading less than his true weight?
A block of mass m is kept on a horizontal ruler. The friction coefficient between the ruler and the block is μ. The ruler is fixed at one end and the block is at a distance L from the fixed end. The ruler is rotated about the fixed end in the horizontal plane through the fixed end. (a) What can the maximum angular speed be for which the block does not slip? (b) If the angular speed of the ruler is uniformly increased from zero at an angular acceleration α, at what angular speed will the block slip?
A person stands on a spring balance at the equator. If the speed of earth's rotation is increased by such an amount that the balance reading is half the true weight, what will be the length of the day in this case?
In a certain unit, the radius of gyration of a uniform disc about its central and transverse axis is `sqrt2.5`. Its radius of gyration about a tangent in its plane (in the same unit) must be ______.
A body slides down a smooth inclined plane having angle θ and reaches the bottom with velocity v. If a body is a sphere, then its linear velocity at the bottom of the plane is
A body of mass m is performing a UCM in a circle of radius r with speed v. The work done by the centripetal force in moving it through `(2/3)`rd of the circular path is ______.
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2 then its resultant accelaration will be ______.
A block of 200 g mass moves with a uniform speed in a horizontal circular groove, with vertical side walls of radius 20 cm. If the block takes 40 s to complete one round, the normal force by the side walls of the groove is ______.
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
