Advertisements
Advertisements
प्रश्न
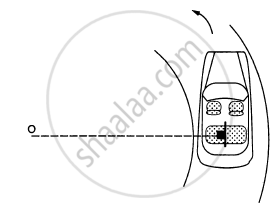
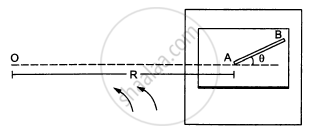
A car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road (In the following figure). A small block of mass 100 g is kept on the seat which rests against the plate. the friction coefficient between the block and the plate is. (a) Find the normal contact force exerted by the plate on the block. (b) The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
उत्तर
Given :
Speed of the car = v = 36 km/h = 10 m/s
Radius of the road = r = 50 m
Friction coefficient between the block and the plate = μ = 0.58
Mass of the small body = m = 100 g = 0.1 kg
(a) Let us find the normal contact force (N) exerted by the plant of the block.
\[N = \frac{\text{mv}^2}{r} = 0 . 1 \times \frac{100}{50} = \frac{1}{5} = 0 . 2\]
(b) The plate is turned; so, the angle between the normal to the plate and the radius of the rod slowly increases.
Therefore, we have :
\[N = \frac{\text{mv}^2}{r}\text{ cos }\theta . . . \left(\text{ i }\right)\]
\[\mu N = \frac{m v^2}{r}\text{ sin }\theta . . . \](ii)
\[\text { On using i and ii , we get : } \]
\[\frac{\mu m v^2}{r}\cos\theta = \frac{\text{mv}^2}{r}\sin\theta\]
\[ \Rightarrow \mu = \text{ tan }\theta\]
\[ \Rightarrow \theta = \tan^{- 1} (0 . 58) \approx 30^\circ\]
APPEARS IN
संबंधित प्रश्न
A smooth block loosely fits in a circular tube placed on a horizontal surface. The block moves in a uniform circular motion along the tube. Which wall (inner or outer) will exert a nonzero normal contact force on the block?
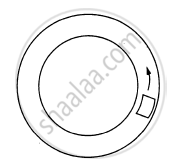
Water in a bucket is whirled in a vertical circle with string attached to it. The water does no fall down even when the bucket is inverted at the top of its path. We conclude that in this position
A coin placed on a rotating turntable just slips. If it is placed at a distance of 4 cm from the centre. If the angular velocity of the turntable is doubled, it will just slip at a distance of
The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
(a) velocity remains constant
(b) speed remains constant
(c) acceleration remains constant
(d) tangential acceleration remains constant.
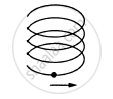
A particle is going in a spiral path as shown in figure with constant speed.
A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
(a) The acceleration of the car is towards the centre of the path.
(b) The magnitude of the frictional force on the car is greater than \[\frac{\text{mv}^2}{\text{r}}\]
(c) The friction coefficient between the ground and the car is not less than a/g.
(d) The friction coefficient between the ground and the car is \[\mu = \tan^{- 1} \frac{\text{v}^2}{\text{rg}.}\]
Find the acceleration of a particle placed on the surface of the earth at the equator due to earth's rotation. The diameter of earth = 12800 km and it takes 24 hours for the earth to complete one revolution about its axis.
A ceiling fan has a diameter (of the circle through the outer edges of the three blades) of 120 cm and rpm 1500 at full speed. Consider a particle of mass 1 g sticking at the outer end of a blade. How much force does it experience when the fan runs at full speed? Who exerts this force on the particle? How much force does the particle exert on the blade along its surface?
The bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the string at this instant.
A person stands on a spring balance at the equator. By what fraction is the balance reading less than his true weight?
A turn of radius 20 m is banked for the vehicles going at a speed of 36 km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
A block of mass m is kept on a horizontal ruler. The friction coefficient between the ruler and the block is μ. The ruler is fixed at one end and the block is at a distance L from the fixed end. The ruler is rotated about the fixed end in the horizontal plane through the fixed end. (a) What can the maximum angular speed be for which the block does not slip? (b) If the angular speed of the ruler is uniformly increased from zero at an angular acceleration α, at what angular speed will the block slip?
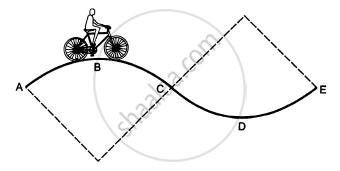
A track consists of two circular parts ABC and CDE of equal radius 100 m and joined smoothly as shown in figure. Each part subtends a right angle at its centre. A cycle weighing 100 kg together with the rider travels at a constant speed of 18 km/h on the track. (a) Find the normal contact force by the road on the cycle when it is at B and at D. (b) Find the force of friction exerted by the track on the tyres when the cycle is at B, C and. (c) Find the normal force between the road and the cycle just before and just after the cycle crosses C. (d) What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g = 10 m/s2.
A particle is projected with a speed u at an angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circular circle? This radius is called the radius of curvature of the curve at the point.
What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes an angle θ/2 with the horizontal?
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular path of radius R (In the following figure). A smooth groove AB of length L(<<R) is made the surface of the table. The groove makes an angle θ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move at the point A in the groove and is released to move along AB. Find the time taken by the particle to reach the point B.
A wheel is subjected to uniform angular acceleration about its axis. The wheel is starting from rest and it rotates through an angle θ1, in first two seconds. In the next two seconds, it rotates through an angle θ2. The ratio θ1/θ2 is ____________.
The escape velocity of a body from any planet, whose mass is six times the mass of earth and radius is twice the radius of earth will be
(v8 = escape velocity of a body from the earth's surface).
A body of M.I. 2 kg m2 rotates with an angular velocity of 20 rad/s. When an external torque of 0.5 N m acts on it in the opposite direction, the number of revolutions it makes before it comes to rest is ____________.
A person driving a car suddenly applies the brakes on seeing a child on the road ahead. If he is not wearing seat belt, he falls forward and hits his head against the steering wheel. Why?
