Advertisements
Advertisements
प्रश्न
A turn of radius 20 m is banked for the vehicles going at a speed of 36 km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
उत्तर
Given:
Speed of vehicles = v = 36 km/hr = 10 m/s
Radius = r = 20 m
Coefficient of static friction = μ = 0.4
Let the road be banked with an angle \[\theta\]
We have :
\[\theta = \tan^{- 1} \frac{\text{v}^2}{\text{rg}}\]
\[ = \tan^{- 1} \frac{100}{20 \times 10}\]
\[ = \tan^{- 1} \left( \frac{1}{2} \right)\]
\[ \Rightarrow \text{tan } \theta = 0 . 5\]
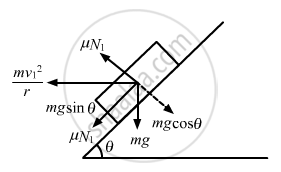
When the car travels at the maximum speed, it slips upward and μN1 acts downward.
Therefore we have :
\[\text{ N}_1 - \text{mg}\cos\theta - \frac{\text{mv}_1^2}{r}\sin\theta = 0 . . . \left( \text{i} \right)\]
\[\mu \text{N}_1 + \text{mg }\sin\theta - \frac{\text{mv}_1^2}{r}\cos\theta = 0 . . . \left(\text{ ii} \right)\]
On solving the above equations, we get :
\[\text{v}_1 = \sqrt{\text{rg}\frac{\mu + \tan\theta}{1 - \mu\tan\theta}}\]
\[ = \sqrt{20 \times 10 \times \frac{0 . 9}{0 . 8}}\]
\[ = 15 \text{ m/s = 54 km/hr }\]
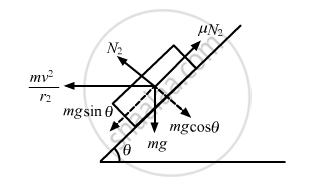
Similarly, for the other case, it can be proved that :
\[\text{v}_2 = \sqrt{\text{rg}\frac{\text{tan}\theta - \mu}{\sqrt{1 - \mu \text{ tan }\theta}}}\]
\[ = \sqrt{20 \times 10 \times \frac{0 . 1}{1 . 2}}\]
\[ = 4 . 08 \text{ m/s = 14 . 7 km/hr}\]
Thus, the possible speeds are between 14.7 km/hr and 54 km/hr so that the car neither slips down nor skids up.
APPEARS IN
संबंधित प्रश्न
A thin circular loop of radius R rotates about its vertical diameter with an angular frequency ω. Show that a small bead on the wire loop remains at its lowermost point for `omega <= sqrt(g/R)` .What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for `omega = sqrt("2g"/R)` ?Neglect friction.
A smooth block loosely fits in a circular tube placed on a horizontal surface. The block moves in a uniform circular motion along the tube. Which wall (inner or outer) will exert a nonzero normal contact force on the block?
Tow cars having masses m1 and m2 moves in circles of radii r1 and r2 respectively. If they complete the circle in equal time, the ratio of their angular speed ω1/ω2 is
Three identical cars A, B and C are moving at the same speed on three bridges. The car A goes on a place bridge, B on a bridge convex upward and C goes on a bridge concave upward. Let FA, FB and FC be the normal forces exerted by the car on the bridges when they are at the middle of bridges.
If the earth stop rotating, the apparent value of g on its surface will
A scooter weighing 150 kg together with its rider moving at 36 km/hr is to take a turn of a radius 30 m. What horizontal force on the scooter is needed to make the turn possible ?
A ceiling fan has a diameter (of the circle through the outer edges of the three blades) of 120 cm and rpm 1500 at full speed. Consider a particle of mass 1 g sticking at the outer end of a blade. How much force does it experience when the fan runs at full speed? Who exerts this force on the particle? How much force does the particle exert on the blade along its surface?
A person stands on a spring balance at the equator. By what fraction is the balance reading less than his true weight?
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
Two particles A and B are located at distances rA and rB respectively from the centre of a rotating disc such that rA > rB. In this case, if angular velocity ω of rotation is constant, then ______
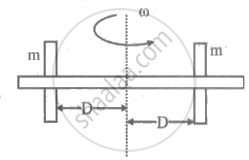
Two identical masses are connected to a horizontal thin (massless) rod as shown in the figure. When their distance from the pivot is D, a torque τ produces an angular acceleration of α1. The masses are now repositioned so that they are 2D from the pivot. The same torque produces an angular acceleration α2 which is given by ______
The escape velocity of a body from any planet, whose mass is six times the mass of earth and radius is twice the radius of earth will be
(v8 = escape velocity of a body from the earth's surface).
A rigid body is rotating with angular velocity 'ω' about an axis of rotation. Let 'v' be the linear velocity of particle which is at perpendicular distance 'r' from the axis of rotation. Then the relation 'v = rω' implies that ______.
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2 then its resultant accelaration will be ______.
An engine is moving on a c1rcular path of radius 200 m with speed of 15 m/s. What will be the frequency heard by an observer who is at rest at the centre of the circular path, when engine blows the whistle with frequency 250 Hz?
A person driving a car suddenly applies the brakes on seeing a child on the road ahead. If he is not wearing seat belt, he falls forward and hits his head against the steering wheel. Why?
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
Define centripetal force.
