Advertisements
Advertisements
प्रश्न
A thin circular loop of radius R rotates about its vertical diameter with an angular frequency ω. Show that a small bead on the wire loop remains at its lowermost point for `omega <= sqrt(g/R)` .What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for `omega = sqrt("2g"/R)` ?Neglect friction.
Advertisements
उत्तर १
Let the radius vector joining the bead with the centre make an angle θ, with the vertical downward direction.
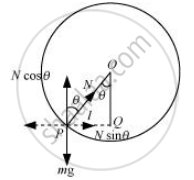
OP = R = Radius of the circle
N = Normal reaction
The respective vertical and horizontal equations of forces can be written as:
mg = Ncosθ ... (i)
mlω2 = Nsinθ … (ii)
In ΔOPQ, we have:
`sin theta = l/R`
`l = Rsin theta`...(iii)
Substiting equation (iii) in equation (ii) we get
m(Rsinθ) ω2 = Nsinθ
mR ω2 = N ... (iv)
Substituting equation (iv) in equation (i), we get:
mg = mR ω2 cosθ
`cos theta = g/(Romega^2)` ...(V)
Since cosθ ≤ 1, the bead will remain at its lowermost point for `g/(Romega^2) <= 1` i.e for `omega <= sqrt(g/R)`
For `omega = sqrt((2g)/R)` or `omega^2 = ((2g)/R)` ..(vi)
On equating equations (v) and (vi), we get:
`(2g)/R = g/(Rcos theta)`
`cos theta = 1/2`
`:. theta = cos^(-1) (0.5 ) = 60^@`
उत्तर २
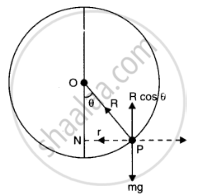
Let the radius vector joining the bead to the centre of the wire make an angle `theta` with the verticle downward dirction. if N is normal reaction, then from fig.
`mg = N cos theta` ....(i)
`mromega^2 = N sin theta` ...(ii)
or `m(R sin theta) omega^2 = N sin theta`
or`mRomega^2 = N`
or `cos theta = g/(Romega^2)`
As |cos theta| <= 1, therefore bead will remain at its lowermost point for
`g/(Romega^2) <= 1 or omega <= sqrt(g/R)`
When `omega = sqrt((2g)/R)` from equation iii
`cos theta = g/R(R/"2g") = 1/2`
`theta = 60^@`
संबंधित प्रश्न
A smooth block loosely fits in a circular tube placed on a horizontal surface. The block moves in a uniform circular motion along the tube. Which wall (inner or outer) will exert a nonzero normal contact force on the block?
A coin placed on a rotating turntable just slips. If it is placed at a distance of 4 cm from the centre. If the angular velocity of the turntable is doubled, it will just slip at a distance of
A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it
Let θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension is the string is mg cos θ
A particle is going in a spiral path as shown in figure with constant speed.
A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
(a) The acceleration of the car is towards the centre of the path.
(b) The magnitude of the frictional force on the car is greater than \[\frac{\text{mv}^2}{\text{r}}\]
(c) The friction coefficient between the ground and the car is not less than a/g.
(d) The friction coefficient between the ground and the car is \[\mu = \tan^{- 1} \frac{\text{v}^2}{\text{rg}.}\]
A ceiling fan has a diameter (of the circle through the outer edges of the three blades) of 120 cm and rpm 1500 at full speed. Consider a particle of mass 1 g sticking at the outer end of a blade. How much force does it experience when the fan runs at full speed? Who exerts this force on the particle? How much force does the particle exert on the blade along its surface?
A particle is projected with a speed u at an angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circular circle? This radius is called the radius of curvature of the curve at the point.
A table with smooth horizontal surface is placed in a circle of a large radius R (In the following figure). A smooth pulley of small radius is fastened to the table. Two masses m and 2m placed on the table are connected through a string going over the pulley. Initially the masses are held by a person with the string along the outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the masses as seen from the cabin and the tension in the string.
Choose the correct option.
Select correct statement about the formula (expression) of moment of inertia (M.I.) in terms of mass M of the object and some of its distance parameter/s, such as R, L, etc.
A body slides down a smooth inclined plane having angle θ and reaches the bottom with velocity v. If a body is a sphere, then its linear velocity at the bottom of the plane is
A particle of mass m is performing UCM along a circle of radius r. The relation between centripetal acceleration a and kinetic energy E is given by
Angular displacement (θ) of a flywheel varies with time as θ = at + bt2 + ct3 then angular acceleration is given by ____________.
If a cyclist doubles his speed while negotiating a curve, how does the tendency to overturn vary?
An engine requires 5 seconds to go from a speed of 600 r.p.m. to 1200 r.p.m. How many revolutions does it make in this period?
When a body slides down from rest along a smooth inclined plane making an angle of 45° with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the co-efficient of friction between the body and the rough plane.
A racing car travels on a track (without banking) ABCDEFA (Figure). ABC is a circular arc of radius 2 R. CD and FA are straight paths of length R and DEF is a circular arc of radius R = 100 m. The co-efficient of friction on the road is µ = 0.1. The maximum speed of the car is 50 ms–1. Find the minimum time for completing one round.
A stone tide to a string of length L is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of change in its velocity, as it reaches a position where the string is horizontal, is `sqrt(x("u"^2 - "gL")`. The value of x is ______.
