Advertisements
Advertisements
प्रश्न
Choose the correct option.
Consider the following cases:
(P) A planet revolving in an elliptical orbit.
(Q) A planet revolving in a circular orbit.
Principle of conservation of angular momentum comes in force in which of these?
विकल्प
Only for (P)
Only for (Q)
For both, (P) and (Q)
Neither for (P), nor for (Q)
उत्तर
For both, (P) and (Q)
Explanation:
The following cases,
- Angular momentum is conserved for any rotating motion rather elliptical or circular.
APPEARS IN
संबंधित प्रश्न
You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘death-well’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m?
When a particle moves in a circle with a uniform speed
Tow cars having masses m1 and m2 moves in circles of radii r1 and r2 respectively. If they complete the circle in equal time, the ratio of their angular speed ω1/ω2 is
A particle is kept fixed on a turntable rotating uniformly. As seen from the ground the particle goes in a circle, its speed is 20 cm/s and acceleration is 20 cm/s2. The particle is now shifted to a new position to make the radius half of the original value. The new value of the speed and acceleration will be
A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it
If the earth stop rotating, the apparent value of g on its surface will
Let θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension is the string is mg cos θ
Assume that the earth goes round the sun in a circular orbit with a constant speed of 30 kms
Find the acceleration of the moon with respect to the earth from the following data:
Distance between the earth and the moon = 3.85 × 105 km and the time taken by the moon to complete one revolution around the earth = 27.3 days.
A stone is fastened to one end of a string and is whirled in a vertical circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
A mosquito is sitting on an L.P. record disc rotating on a turn table at \[33\frac{1}{3}\] revolutions per minute. The distance of the mosquito from the centre of the turn table is 10 cm. Show that the friction coefficient between the record and the mosquito is greater than π2/81. Take g =10 m/s2.
Suppose the bob of the previous problem has a speed of 1.4 m/s when the string makes an angle of 0.20 radian with the vertical. Find the tension at this instant. You can use cos θ ≈ 1 − θ2/2 and SINθ ≈ θ for small θ.
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
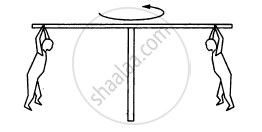
In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod (In the following figure). Let the mass of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
A hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical. A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is μ. Find the range of the angular speed for which the block will not slip.
A particle is projected with a speed u at an angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circular circle? This radius is called the radius of curvature of the curve at the point.
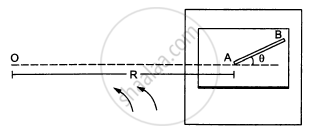
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular path of radius R (In the following figure). A smooth groove AB of length L(<<R) is made the surface of the table. The groove makes an angle θ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move at the point A in the groove and is released to move along AB. Find the time taken by the particle to reach the point B.
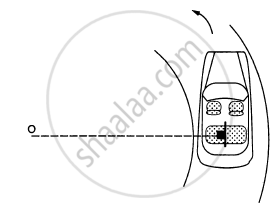
A car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road (In the following figure). A small block of mass 100 g is kept on the seat which rests against the plate. the friction coefficient between the block and the plate is. (a) Find the normal contact force exerted by the plate on the block. (b) The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
A person stands on a spring balance at the equator. If the speed of earth's rotation is increased by such an amount that the balance reading is half the true weight, what will be the length of the day in this case?
When seen from below, the blades of a ceiling fan are seen to be revolving anticlockwise and their speed is decreasing. Select the correct statement about the directions of its angular velocity and angular acceleration.
In non-uniform circular motion, the ratio of tangential to radial acceleration is (r = radius, a = angular acceleration and v = linear velocity)
Two particles A and B are located at distances rA and rB respectively from the centre of a rotating disc such that rA > rB. In this case, if angular velocity ω of rotation is constant, then ______
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2, then its resultant acceleration will be ______.
The real force 'F' acting on a particle of mass ' m' performing circular motion acts along the radius of circle 'r' and is directed towards the centre of circle. The square root of the magnitude of such force is (T = periodic time).
If a cyclist doubles his speed while negotiating a curve, how does the tendency to overturn vary?
An engine requires 5 seconds to go from a speed of 600 r.p.m. to 1200 r.p.m. How many revolutions does it make in this period?
