Advertisements
Advertisements
प्रश्न
A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it
विकल्प
increases
decreases
remains the same
fluctuates.
उत्तर

The normal force on the motorcycle , \[\text{N = mg}\cos\theta - \frac{\text{mv}^2}{R}\]
As the motorcycle is ascending on the overbridge, θ decreases (from \[\frac{\pi}{2}\] to 0).
So, normal force increases with decrease in θ.
APPEARS IN
संबंधित प्रश्न
A particle is kept fixed on a turntable rotating uniformly. As seen from the ground the particle goes in a circle, its speed is 20 cm/s and acceleration is 20 cm/s2. The particle is now shifted to a new position to make the radius half of the original value. The new value of the speed and acceleration will be
Three identical cars A, B and C are moving at the same speed on three bridges. The car A goes on a place bridge, B on a bridge convex upward and C goes on a bridge concave upward. Let FA, FB and FC be the normal forces exerted by the car on the bridges when they are at the middle of bridges.
A simple pendulum having a bob of mass m is suspended from the ceiling of a car used in a stunt film shooting. the car moves up along an inclined cliff at a speed v and makes a jump to leave the cliff and lands at some distance. Let R be the maximum height of the car from the top of the cliff. The tension in the string when the car is in air is
The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
(a) velocity remains constant
(b) speed remains constant
(c) acceleration remains constant
(d) tangential acceleration remains constant.
A particle is going in a spiral path as shown in figure with constant speed.
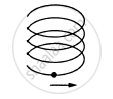
A particle moves in a circle of radius 1.0 cm at a speed given by v = 2.0 t where v is cm/s and t in seconds.
(a) Find the radial acceleration of the particle at t = 1 s.
(b) Find the tangential acceleration at t = 1 s.
(c) Find the magnitude of the acceleration at t = 1 s.
A ceiling fan has a diameter (of the circle through the outer edges of the three blades) of 120 cm and rpm 1500 at full speed. Consider a particle of mass 1 g sticking at the outer end of a blade. How much force does it experience when the fan runs at full speed? Who exerts this force on the particle? How much force does the particle exert on the blade along its surface?
Suppose the bob of the previous problem has a speed of 1.4 m/s when the string makes an angle of 0.20 radian with the vertical. Find the tension at this instant. You can use cos θ ≈ 1 − θ2/2 and SINθ ≈ θ for small θ.
What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes an angle θ/2 with the horizontal?
A block of mass m moves on a horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v writes
(a) the normal force by the wall on the block,
(b) the frictional force by a wall, and
(c) the tangential acceleration of the block.
(d) Integrate the tangential acceleration \[\left( \frac{dv}{dt} = v\frac{dv}{ds} \right)\] to obtain the speed of the block after one revolution.
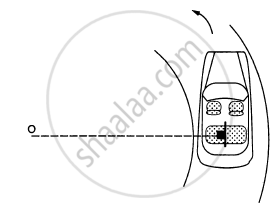
A car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road (In the following figure). A small block of mass 100 g is kept on the seat which rests against the plate. the friction coefficient between the block and the plate is. (a) Find the normal contact force exerted by the plate on the block. (b) The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
A particle of mass 1 kg, tied to a 1.2 m long string is whirled to perform the vertical circular motion, under gravity. The minimum speed of a particle is 5 m/s. Consider the following statements.
P) Maximum speed must be `5sqrt5` m/s.
Q) Difference between maximum and minimum tensions along the string is 60 N.
Select the correct option.
Choose the correct option.
Select correct statement about the formula (expression) of moment of inertia (M.I.) in terms of mass M of the object and some of its distance parameter/s, such as R, L, etc.
Choose the correct option.
Consider the following cases:
(P) A planet revolving in an elliptical orbit.
(Q) A planet revolving in a circular orbit.
Principle of conservation of angular momentum comes in force in which of these?
Two particles A and B are located at distances rA and rB respectively from the centre of a rotating disc such that rA > rB. In this case, if angular velocity ω of rotation is constant, then ______
The real force 'F' acting on a particle of mass ' m' performing circular motion acts along the radius of circle 'r' and is directed towards the centre of circle. The square root of the magnitude of such force is (T = periodic time).
In negotiating curve on a flat road, a cyclist leans inwards by an angle e with the vertical in order to ______.
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2 then its resultant accelaration will be ______.
Statement I: A cyclist is moving on an unbanked road with a speed of 7 kmh-1 and takes a sharp circular turn along a path of radius of 2 m without reducing the speed. The static friction coefficient is 0.2. The cyclist will not slip and pass the curve. (g = 9.8 m/s2)
Statement II: If the road is banked at an angle of 45°, cyclist can cross the curve of 2 m radius with the speed of 18.5 kmh-1 without slipping.
In the light of the above statements, choose the correct answer from the options given below.
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
