Advertisements
Advertisements
प्रश्न
A particle moves in a circle of radius 1.0 cm at a speed given by v = 2.0 t where v is cm/s and t in seconds.
(a) Find the radial acceleration of the particle at t = 1 s.
(b) Find the tangential acceleration at t = 1 s.
(c) Find the magnitude of the acceleration at t = 1 s.
उत्तर
Speed is given as a function of time. Therefore, we have:
v = 2t
Radius of the circle = r = 1 cm
At time t = 2 s, we get :
(a) Radial acceleration
\[\text{a} = \frac{\text{v}^2}{\text{r}} = \frac{2 {}^2}{1} = 4 \text{ cm/ s}^2\]
(b) Tangential acceleration
\[\text{a} = \frac{\text{dv}}{\text{dt}}\]
\[ = \frac{d}{\text{{dt}}}\left( 2t \right) = 2 \text{ cm/ s}^2\]
(c) Magnitude of acceleration
\[a = \sqrt{4^2 + 2^2}\]
\[ = \sqrt{20} \text{ cm/ s}^2\]
APPEARS IN
संबंधित प्रश्न
A smooth block loosely fits in a circular tube placed on a horizontal surface. The block moves in a uniform circular motion along the tube. Which wall (inner or outer) will exert a nonzero normal contact force on the block?
When a particle moves in a circle with a uniform speed
A coin placed on a rotating turntable just slips. If it is placed at a distance of 4 cm from the centre. If the angular velocity of the turntable is doubled, it will just slip at a distance of
A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it
Assume that the earth goes round the sun in a circular orbit with a constant speed of 30 kms
A stone is fastened to one end of a string and is whirled in a vertical circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
A ceiling fan has a diameter (of the circle through the outer edges of the three blades) of 120 cm and rpm 1500 at full speed. Consider a particle of mass 1 g sticking at the outer end of a blade. How much force does it experience when the fan runs at full speed? Who exerts this force on the particle? How much force does the particle exert on the blade along its surface?
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
A block of mass m is kept on a horizontal ruler. The friction coefficient between the ruler and the block is μ. The ruler is fixed at one end and the block is at a distance L from the fixed end. The ruler is rotated about the fixed end in the horizontal plane through the fixed end. (a) What can the maximum angular speed be for which the block does not slip? (b) If the angular speed of the ruler is uniformly increased from zero at an angular acceleration α, at what angular speed will the block slip?
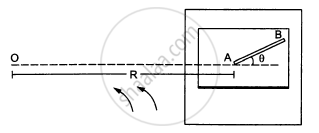
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular path of radius R (In the following figure). A smooth groove AB of length L(<<R) is made the surface of the table. The groove makes an angle θ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move at the point A in the groove and is released to move along AB. Find the time taken by the particle to reach the point B.
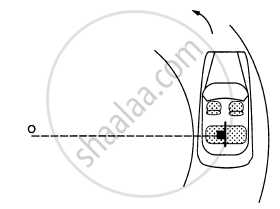
A car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road (In the following figure). A small block of mass 100 g is kept on the seat which rests against the plate. the friction coefficient between the block and the plate is. (a) Find the normal contact force exerted by the plate on the block. (b) The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
In a certain unit, the radius of gyration of a uniform disc about its central and transverse axis is `sqrt2.5`. Its radius of gyration about a tangent in its plane (in the same unit) must be ______.
The real force 'F' acting on a particle of mass ' m' performing circular motion acts along the radius of circle 'r' and is directed towards the centre of circle. The square root of the magnitude of such force is (T = periodic time).
A body of mass m is performing a UCM in a circle of radius r with speed v. The work done by the centripetal force in moving it through `(2/3)`rd of the circular path is ______.
In negotiating curve on a flat road, a cyclist leans inwards by an angle e with the vertical in order to ______.
An engine is moving on a c1rcular path of radius 200 m with speed of 15 m/s. What will be the frequency heard by an observer who is at rest at the centre of the circular path, when engine blows the whistle with frequency 250 Hz?
When a body slides down from rest along a smooth inclined plane making an angle of 45° with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the co-efficient of friction between the body and the rough plane.
A stone tide to a string of length L is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of change in its velocity, as it reaches a position where the string is horizontal, is `sqrt(x("u"^2 - "gL")`. The value of x is ______.
Find the angular acceleration of a particle in circular motion which slows down from 300 r.p.m. to 0 r.p.m. in 20 s.
