Advertisements
Advertisements
प्रश्न
In a certain unit, the radius of gyration of a uniform disc about its central and transverse axis is `sqrt2.5`. Its radius of gyration about a tangent in its plane (in the same unit) must be ______.
विकल्प
`sqrt5`
2.5
`2sqrt2.5`
`sqrt12.5`
उत्तर
In a certain unit, the radius of gyration of a uniform disc about its central and transverse axis is `sqrt2.5`. Its radius of gyration about a tangent in its plane (in the same unit) must be 2.5.
Explanation:
Expression for M.I of a uniform disc about its central and transverse axis is given by:
M.I = `(m xx R^2)/2` ......(i)
Here, m and R are mass and radius of gyration respectively.
Let K be the radius of gyration of disc. Then, from (i) we can write,
M.I = `(m xx R^2)/2`
`m xx K^2 = (m xx R^2)/2`
`K = R/sqrt(2)`
Therefore, `sqrt2.5 = R/sqrt(2)`
`R = sqrt(5)` ......(ii)
Now, Expression for moment of inertia of uniform disc about tangent is given by:
M.I = `(5mR^2)/4`
If K' be the radius of gyration of disc about tangent then we can write:
M.I = `(5mR^2)/4`
m × (K')2 = `(5mR^2)/4`
(K')2 = `(5R^2)/4`
(K')2 = `(5(sqrt5)^2)/4`
(K')2 = `(5 xx 5)/4`
(K')2 = `25/4`
(K')2 = 2.5
APPEARS IN
संबंधित प्रश्न
A thin circular loop of radius R rotates about its vertical diameter with an angular frequency ω. Show that a small bead on the wire loop remains at its lowermost point for `omega <= sqrt(g/R)` .What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for `omega = sqrt("2g"/R)` ?Neglect friction.
A smooth block loosely fits in a circular tube placed on a horizontal surface. The block moves in a uniform circular motion along the tube. Which wall (inner or outer) will exert a nonzero normal contact force on the block?
Tow cars having masses m1 and m2 moves in circles of radii r1 and r2 respectively. If they complete the circle in equal time, the ratio of their angular speed ω1/ω2 is
A stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it
The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
(a) velocity remains constant
(b) speed remains constant
(c) acceleration remains constant
(d) tangential acceleration remains constant.
Find the acceleration of the moon with respect to the earth from the following data:
Distance between the earth and the moon = 3.85 × 105 km and the time taken by the moon to complete one revolution around the earth = 27.3 days.
A particle moves in a circle of radius 1.0 cm at a speed given by v = 2.0 t where v is cm/s and t in seconds.
(a) Find the radial acceleration of the particle at t = 1 s.
(b) Find the tangential acceleration at t = 1 s.
(c) Find the magnitude of the acceleration at t = 1 s.
A ceiling fan has a diameter (of the circle through the outer edges of the three blades) of 120 cm and rpm 1500 at full speed. Consider a particle of mass 1 g sticking at the outer end of a blade. How much force does it experience when the fan runs at full speed? Who exerts this force on the particle? How much force does the particle exert on the blade along its surface?
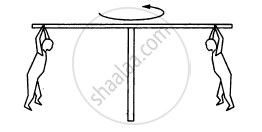
In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod (In the following figure). Let the mass of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
A person stands on a spring balance at the equator. If the speed of earth's rotation is increased by such an amount that the balance reading is half the true weight, what will be the length of the day in this case?
Choose the correct option.
Select correct statement about the formula (expression) of moment of inertia (M.I.) in terms of mass M of the object and some of its distance parameter/s, such as R, L, etc.
A body slides down a smooth inclined plane having angle θ and reaches the bottom with velocity v. If a body is a sphere, then its linear velocity at the bottom of the plane is
A child starts running from rest along a circular track of radius r with constant tangential acceleration a. After time the feels that slipping of shoes on the ground has started. The coefficient of friction between shoes and the ground is [g = acceleration due to gravity].
The centripetal force of a body moving in a circular path, if speed is made half and radius is made four times the original value, will ____________.
A rigid body is rotating with angular velocity 'ω' about an axis of rotation. Let 'v' be the linear velocity of particle which is at perpendicular distance 'r' from the axis of rotation. Then the relation 'v = rω' implies that ______.
If a cyclist doubles his speed while negotiating a curve, how does the tendency to overturn vary?
A body of mass m is performing a UCM in a circle of radius r with speed v. The work done by the centripetal force in moving it through `(2/3)`rd of the circular path is ______.
A body of M.I. 2 kg m2 rotates with an angular velocity of 20 rad/s. When an external torque of 0.5 N m acts on it in the opposite direction, the number of revolutions it makes before it comes to rest is ____________.
In negotiating curve on a flat road, a cyclist leans inwards by an angle e with the vertical in order to ______.
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2 then its resultant accelaration will be ______.
An engine is moving on a c1rcular path of radius 200 m with speed of 15 m/s. What will be the frequency heard by an observer who is at rest at the centre of the circular path, when engine blows the whistle with frequency 250 Hz?
A person driving a car suddenly applies the brakes on seeing a child on the road ahead. If he is not wearing seat belt, he falls forward and hits his head against the steering wheel. Why?
A stone tide to a string of length L is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of change in its velocity, as it reaches a position where the string is horizontal, is `sqrt(x("u"^2 - "gL")`. The value of x is ______.
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
Define centripetal force.
