Advertisements
Advertisements
प्रश्न
A ceiling fan has a diameter (of the circle through the outer edges of the three blades) of 120 cm and rpm 1500 at full speed. Consider a particle of mass 1 g sticking at the outer end of a blade. How much force does it experience when the fan runs at full speed? Who exerts this force on the particle? How much force does the particle exert on the blade along its surface?
उत्तर
Diameter of the fan = 120 cm
∴ Radius of the fan = r = 60 cm = 0.6 m
Mass of the particle = M = 1 g = 0.001 kg
Frequency of revolutions = n = 1500 rev/min = 25 rev/s
Angular velocity = ω = 2\[\pi\]n = 2\[\pi\] × 25 = 57.14 rev/s
Force of the blade on the particle:
F = Mrw2
= (0.001) × 0.6 × (157.14)2
=14.8 N
The moving fan exerts this force on the particle.
The particle also exerts a force of 14.8 N on the blade along its surface.
APPEARS IN
संबंधित प्रश्न
You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘death-well’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m?
Water in a bucket is whirled in a vertical circle with string attached to it. The water does no fall down even when the bucket is inverted at the top of its path. We conclude that in this position
A stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
An object follows a curved path. The following quantities may remain constant during the motion
(a) speed
(b) velocity
(c) acceleration
(d) magnitude of acceleration.
A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
(a) The acceleration of the car is towards the centre of the path.
(b) The magnitude of the frictional force on the car is greater than \[\frac{\text{mv}^2}{\text{r}}\]
(c) The friction coefficient between the ground and the car is not less than a/g.
(d) The friction coefficient between the ground and the car is \[\mu = \tan^{- 1} \frac{\text{v}^2}{\text{rg}.}\]
A simple pendulum is suspended from the ceiling of a car taking a turn of radius 10 m at a speed of 36 km/h. Find the angle made by he string of the pendulum with the vertical if this angle does not change during the turn. Take g = 10 m/s2.
Suppose the bob of the previous problem has a speed of 1.4 m/s when the string makes an angle of 0.20 radian with the vertical. Find the tension at this instant. You can use cos θ ≈ 1 − θ2/2 and SINθ ≈ θ for small θ.
A turn of radius 20 m is banked for the vehicles going at a speed of 36 km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
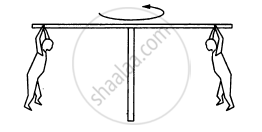
In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod (In the following figure). Let the mass of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
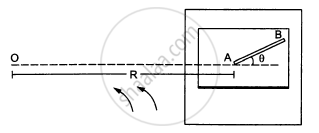
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular path of radius R (In the following figure). A smooth groove AB of length L(<<R) is made the surface of the table. The groove makes an angle θ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move at the point A in the groove and is released to move along AB. Find the time taken by the particle to reach the point B.
When seen from below, the blades of a ceiling fan are seen to be revolving anticlockwise and their speed is decreasing. Select the correct statement about the directions of its angular velocity and angular acceleration.
Choose the correct option.
Consider the following cases:
(P) A planet revolving in an elliptical orbit.
(Q) A planet revolving in a circular orbit.
Principle of conservation of angular momentum comes in force in which of these?
A particle is moving in a radius R with constant speed v. The magnitude of average acceleration after half revolution is ____________.
The real force 'F' acting on a particle of mass ' m' performing circular motion acts along the radius of circle 'r' and is directed towards the centre of circle. The square root of the magnitude of such force is (T = periodic time).
A rigid body is rotating with angular velocity 'ω' about an axis of rotation. Let 'v' be the linear velocity of particle which is at perpendicular distance 'r' from the axis of rotation. Then the relation 'v = rω' implies that ______.
Angular displacement (θ) of a flywheel varies with time as θ = at + bt2 + ct3 then angular acceleration is given by ____________.
If a cyclist doubles his speed while negotiating a curve, how does the tendency to overturn vary?
A block of 200 g mass moves with a uniform speed in a horizontal circular groove, with vertical side walls of radius 20 cm. If the block takes 40 s to complete one round, the normal force by the side walls of the groove is ______.
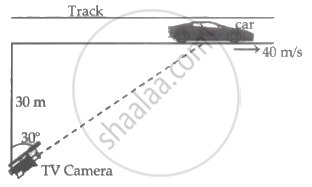
A racing car is travelling along a track at a constant speed of 40 m/s. A T.V. cameraman is recording the event from a distance of 30 m directly away from the track as shown in the figure. In order to keep the car under view in the position shown, the angular speed with which the camera should be rotated is ______.