Advertisements
Advertisements
प्रश्न
In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod (In the following figure). Let the mass of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
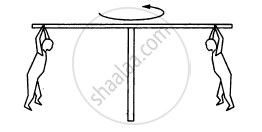
उत्तर
Given :
\[\text {Frequency of rod }= n = 20 \text{ rev} \text{ per } \min\]
\[ \Rightarrow \text{ n} = \frac{20}{60} = \frac{1}{3}\text{rev/s}\]
Therefore, we have :
angular velocity of rod ,
\[\text { Angular velocity of rod }= \omega = 2\pi n = \frac{2\pi}{3}\text{rad/s}\]
Mass of each kid = \[\text{m = 15 kg}\]
Radius = \[r = \frac{3}{2} = 1 . 5 \text{m}\]
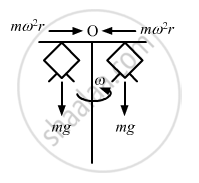
\[\therefore \text { Frictional force }= F = \text{mr }\omega^2 \]
\[ \Rightarrow F = 15 \times (1 . 5) \times \frac{(2\pi )^2}{9}\]
\[ = 5 \times (0 . 5) \times 4 \pi^2 = 10 \pi^2 N\]
Thus, the force of frictional on one of the kids is 10 \[\pi\]
APPEARS IN
संबंधित प्रश्न
You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘death-well’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m?
A 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
An object follows a curved path. The following quantities may remain constant during the motion
(a) speed
(b) velocity
(c) acceleration
(d) magnitude of acceleration.
Find the acceleration of a particle placed on the surface of the earth at the equator due to earth's rotation. The diameter of earth = 12800 km and it takes 24 hours for the earth to complete one revolution about its axis.
A stone is fastened to one end of a string and is whirled in a vertical circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
Suppose the bob of the previous problem has a speed of 1.4 m/s when the string makes an angle of 0.20 radian with the vertical. Find the tension at this instant. You can use cos θ ≈ 1 − θ2/2 and SINθ ≈ θ for small θ.
Suppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
A block of mass m moves on a horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v writes
(a) the normal force by the wall on the block,
(b) the frictional force by a wall, and
(c) the tangential acceleration of the block.
(d) Integrate the tangential acceleration \[\left( \frac{dv}{dt} = v\frac{dv}{ds} \right)\] to obtain the speed of the block after one revolution.
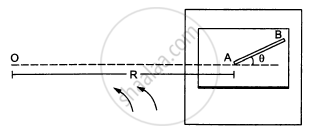
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular path of radius R (In the following figure). A smooth groove AB of length L(<<R) is made the surface of the table. The groove makes an angle θ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move at the point A in the groove and is released to move along AB. Find the time taken by the particle to reach the point B.
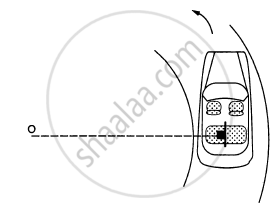
A car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road (In the following figure). A small block of mass 100 g is kept on the seat which rests against the plate. the friction coefficient between the block and the plate is. (a) Find the normal contact force exerted by the plate on the block. (b) The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
Choose the correct option.
Consider the following cases:
(P) A planet revolving in an elliptical orbit.
(Q) A planet revolving in a circular orbit.
Principle of conservation of angular momentum comes in force in which of these?
A particle of mass m is performing UCM along a circle of radius r. The relation between centripetal acceleration a and kinetic energy E is given by
A rope is wound around a solid cylinder of mass 1 kg and radius 0.4 m. What is the angular acceleration of cylinder, if the rope is pulled with a force of 25 N? (Cylinder is rotating about its own axis.)
A body of M.I. 2 kg m2 rotates with an angular velocity of 20 rad/s. When an external torque of 0.5 N m acts on it in the opposite direction, the number of revolutions it makes before it comes to rest is ____________.
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2 then its resultant accelaration will be ______.
When a body slides down from rest along a smooth inclined plane making an angle of 45° with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the co-efficient of friction between the body and the rough plane.
A racing car travels on a track (without banking) ABCDEFA (Figure). ABC is a circular arc of radius 2 R. CD and FA are straight paths of length R and DEF is a circular arc of radius R = 100 m. The co-efficient of friction on the road is µ = 0.1. The maximum speed of the car is 50 ms–1. Find the minimum time for completing one round.

Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
