Advertisements
Advertisements
प्रश्न
A hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical. A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is μ. Find the range of the angular speed for which the block will not slip.
उत्तर
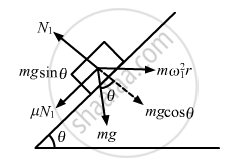
When the bowl rotates at maximum angular speed, the block tends to slip upwards.
Also, the frictional force acts downward.
Here, we have:
Radius of the path that the block follow = r = Rsinθ
Let N1 be the normal reaction on the block and ω1 be the angular velocity after which the block will slip.
From the free body diagram-1, we get :
\[N_1 - \text{mg}\cos\theta = {m\omega}_1^2 (R\sin\theta)\sin\theta . . . \](i)
\[\mu N_1 + \text{mg}sin\theta = m \omega_1^2 (R\sin\theta)\cos\theta . . . \](ii)
On solving the two equation, we get :
\[\omega_1 = \left[ \frac{g(\text{sin}\theta + \mu\text{ cos}\theta)}{\text{R sin}\theta (\text{cos}\theta - \mu \text{ sin }\theta)} \right]^{1/2}\]
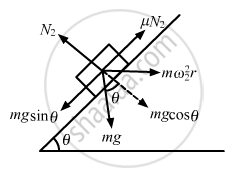
Let us now find the minimum speed (ω2) on altering the direction of \[\mu\] (as shown in figure):
\[\omega_2 = \left[ \frac{g(\text{ sin }\theta - \mu \text{ cos }\theta)}{\text{R sin}\theta (\text{ cos }\theta + \mu \text{ sin }\theta)} \right]^{1/2}\]
Hence, the range of speed is between ω2 and ω1.
APPEARS IN
संबंधित प्रश्न
You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘death-well’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m?
A particle is kept fixed on a turntable rotating uniformly. As seen from the ground the particle goes in a circle, its speed is 20 cm/s and acceleration is 20 cm/s2. The particle is now shifted to a new position to make the radius half of the original value. The new value of the speed and acceleration will be
A stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
Let θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension is the string is mg cos θ
Assume that the earth goes round the sun in a circular orbit with a constant speed of 30 kms
The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
(a) velocity remains constant
(b) speed remains constant
(c) acceleration remains constant
(d) tangential acceleration remains constant.
A particle moves in a circle of radius 1.0 cm at a speed given by v = 2.0 t where v is cm/s and t in seconds.
(a) Find the radial acceleration of the particle at t = 1 s.
(b) Find the tangential acceleration at t = 1 s.
(c) Find the magnitude of the acceleration at t = 1 s.
A ceiling fan has a diameter (of the circle through the outer edges of the three blades) of 120 cm and rpm 1500 at full speed. Consider a particle of mass 1 g sticking at the outer end of a blade. How much force does it experience when the fan runs at full speed? Who exerts this force on the particle? How much force does the particle exert on the blade along its surface?
What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes an angle θ/2 with the horizontal?
When seen from below, the blades of a ceiling fan are seen to be revolving anticlockwise and their speed is decreasing. Select the correct statement about the directions of its angular velocity and angular acceleration.
A body slides down a smooth inclined plane having angle θ and reaches the bottom with velocity v. If a body is a sphere, then its linear velocity at the bottom of the plane is
The escape velocity of a body from any planet, whose mass is six times the mass of earth and radius is twice the radius of earth will be
(v8 = escape velocity of a body from the earth's surface).
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2, then its resultant acceleration will be ______.
The centripetal force of a body moving in a circular path, if speed is made half and radius is made four times the original value, will ____________.
Angular displacement (θ) of a flywheel varies with time as θ = at + bt2 + ct3 then angular acceleration is given by ____________.
If a cyclist doubles his speed while negotiating a curve, how does the tendency to overturn vary?
A particle performs uniform circular motion in a horizontal plane. The radius of the circle is 10 cm. If the centripetal force F is kept constant but the angular velocity is halved, the new radius of the path will be ______.
A body of mass m is performing a UCM in a circle of radius r with speed v. The work done by the centripetal force in moving it through `(2/3)`rd of the circular path is ______.
A person driving a car suddenly applies the brakes on seeing a child on the road ahead. If he is not wearing seat belt, he falls forward and hits his head against the steering wheel. Why?
