Advertisements
Advertisements
प्रश्न
A particle of mass 1 kg, tied to a 1.2 m long string is whirled to perform the vertical circular motion, under gravity. The minimum speed of a particle is 5 m/s. Consider the following statements.
P) Maximum speed must be `5sqrt5` m/s.
Q) Difference between maximum and minimum tensions along the string is 60 N.
Select the correct option.
विकल्प
Only the statement P is correct.
Only the statement Q is correct.
Both the statements are correct.
Both the statements are incorrect.
उत्तर
Only the statement Q is correct.
Explanation:
The minimum speed of the particle = `v_"A"` = 5 m/s
The length of the string (h) = 2.4 m
The radius (l) = 1.2 m
The mass of the particle, m = 1 kg
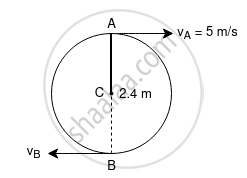
Conserving energy between A and B
`=> 1/2 mv_"A"^2 + mgh = 1/2mv_"B"^2 + 0`
`=> v_"A"^2 + 2gh = v_"B"^2`
`=> 5^2 + 2 xx 9.8 xx 2.4 = v_"B"^2`
`=> v_"B"^2 = 72`
`=> v_"B" = sqrt72` m/s
At point B,
`T_B - mg = (mv_"B"^2)/r`
`T_B = (mv_"B"^2)/r + mg` ...(1)
At point A,
`T_A + mg = (mv_"A"^2)/r`
`T_A = (mv_"A"^2)/r - mg` ...(2)
`T_B - T_A = ((mv_"B"^2)/r + mg) - ((mv_"A"^2)/r - mg)`
`= m/r (v_"B"^2 - v_"A"^2) + 2mg`
`= 1/1.2 (72 - 25) + 2(1)(9.8)`
= 60 N
संबंधित प्रश्न
A stone of mass 0.25 kg tied to the end of a string is whirled round in a circle of radius 1.5 m with a speed of 40 rev/min in a horizontal plane. What is the tension in the string? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
A smooth block loosely fits in a circular tube placed on a horizontal surface. The block moves in a uniform circular motion along the tube. Which wall (inner or outer) will exert a nonzero normal contact force on the block?
Three identical cars A, B and C are moving at the same speed on three bridges. The car A goes on a place bridge, B on a bridge convex upward and C goes on a bridge concave upward. Let FA, FB and FC be the normal forces exerted by the car on the bridges when they are at the middle of bridges.
A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
An object follows a curved path. The following quantities may remain constant during the motion
(a) speed
(b) velocity
(c) acceleration
(d) magnitude of acceleration.
The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
(a) velocity remains constant
(b) speed remains constant
(c) acceleration remains constant
(d) tangential acceleration remains constant.
A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
(a) The acceleration of the car is towards the centre of the path.
(b) The magnitude of the frictional force on the car is greater than \[\frac{\text{mv}^2}{\text{r}}\]
(c) The friction coefficient between the ground and the car is not less than a/g.
(d) The friction coefficient between the ground and the car is \[\mu = \tan^{- 1} \frac{\text{v}^2}{\text{rg}.}\]
A stone is fastened to one end of a string and is whirled in a vertical circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
A simple pendulum is suspended from the ceiling of a car taking a turn of radius 10 m at a speed of 36 km/h. Find the angle made by he string of the pendulum with the vertical if this angle does not change during the turn. Take g = 10 m/s2.
The bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the string at this instant.
Suppose the bob of the previous problem has a speed of 1.4 m/s when the string makes an angle of 0.20 radian with the vertical. Find the tension at this instant. You can use cos θ ≈ 1 − θ2/2 and SINθ ≈ θ for small θ.
A person stands on a spring balance at the equator. By what fraction is the balance reading less than his true weight?
A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate \[\frac{\text{dv}}{\text{dt}} = a\] . The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.
A block of mass m moves on a horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v writes
(a) the normal force by the wall on the block,
(b) the frictional force by a wall, and
(c) the tangential acceleration of the block.
(d) Integrate the tangential acceleration \[\left( \frac{dv}{dt} = v\frac{dv}{ds} \right)\] to obtain the speed of the block after one revolution.
A person stands on a spring balance at the equator. If the speed of earth's rotation is increased by such an amount that the balance reading is half the true weight, what will be the length of the day in this case?
When seen from below, the blades of a ceiling fan are seen to be revolving anticlockwise and their speed is decreasing. Select the correct statement about the directions of its angular velocity and angular acceleration.
In non-uniform circular motion, the ratio of tangential to radial acceleration is (r = radius, a = angular acceleration and v = linear velocity)
A particle of mass m is performing UCM along a circle of radius r. The relation between centripetal acceleration a and kinetic energy E is given by
A rope is wound around a solid cylinder of mass 1 kg and radius 0.4 m. What is the angular acceleration of cylinder, if the rope is pulled with a force of 25 N? (Cylinder is rotating about its own axis.)
The real force 'F' acting on a particle of mass ' m' performing circular motion acts along the radius of circle 'r' and is directed towards the centre of circle. The square root of the magnitude of such force is (T = periodic time).
Angular displacement (θ) of a flywheel varies with time as θ = at + bt2 + ct3 then angular acceleration is given by ____________.
If a cyclist doubles his speed while negotiating a curve, how does the tendency to overturn vary?
A body of mass m is performing a UCM in a circle of radius r with speed v. The work done by the centripetal force in moving it through `(2/3)`rd of the circular path is ______.
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2 then its resultant accelaration will be ______.
When a body slides down from rest along a smooth inclined plane making an angle of 45° with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the co-efficient of friction between the body and the rough plane.
