Advertisements
Advertisements
Question
There are three forces F1, F2 and F3 acting on a body, all acting on a point P on the body. The body is found to move with uniform speed.
- Show that the forces are coplanar.
- Show that the torque acting on the body about any point due to these three forces is zero.
Solution
As the body is moving with uniform speed (velocity) its acceleration a = 0.
∴ The sum of the forces is zero, F1 + F2 + F3 = 0
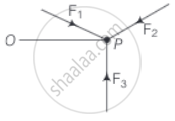
a. Let F1, F2 and F3 be the three forces passing through a point. Let F1, and F2, be in plane A (one can always draw a plane having two intersecting lines such that the two lines lie on the plane). Then F1 + F2 must be in plane A. Since, F3 = – (F1 + F2), F3 is also in plane A.
b. Consider the torque of the forces about P Since, all the forces pass through P, the torque is zero. Now, consider torque about another point O. Then torque about O is Torque = OP × (F1 + F2 + F3). Since, F1 + F2 + F3 = 0, torque = 0.
APPEARS IN
RELATED QUESTIONS
Explain why it is easier to pull a lawn mower than to push it.
A mass m is suspended from a rigid support P by means of a massless string as shown in figure. A horizontal force F is applied at point O of the rope. The system is in equilibrium when the string makes an angle θ with the vertical. Then the relation between the tension T, force F and angle θ is P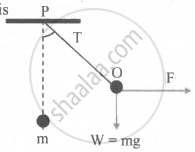
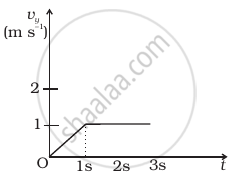
Figure shows (vx, t) and (vy, t) diagrams for a body of unit mass. Find the force as a function of time.
 (a) |
 (b) |
There are four forces acting at a point P produced by strings as shown in the figure, which is at rest. Find the forces F1 and F2.

