Advertisements
Advertisements
Question
There are four forces acting at a point P produced by strings as shown in the figure, which is at rest. Find the forces F1 and F2.

Solution
Consider the adjacent diagram, in which forces are resolved.
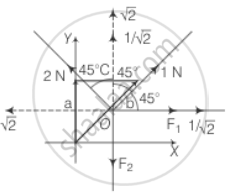
On resolving forces into rectangular components, in equilibrium forces `(F_1 + 1/sqrt(2))` N are equal to `sqrt(2)` N and F2 is equal to `(sqrt(2) + 1/sqrt(2))` N.
∴ `F_1 + 1/sqrt(2) = sqrt(2)`
`F_1 = sqrt(2) - 1/sqrt(2)`
= `(2 - 1)/sqrt(2)`
= `1/sqrt(2)`
= 0.707 N
And `F_2 = sqrt(2) + 1/sqrt(2)`
= `(2 + 1)/sqrt(2)` N
= `3/sqrt(2)` N
= 2.121 N
APPEARS IN
RELATED QUESTIONS
Explain why it is easier to pull a lawn mower than to push it.
A mass m is suspended from a rigid support P by means of a massless string as shown in figure. A horizontal force F is applied at point O of the rope. The system is in equilibrium when the string makes an angle θ with the vertical. Then the relation between the tension T, force F and angle θ is P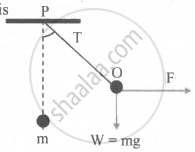
There are three forces F1, F2 and F3 acting on a body, all acting on a point P on the body. The body is found to move with uniform speed.
- Show that the forces are coplanar.
- Show that the torque acting on the body about any point due to these three forces is zero.
Figure shows (vx, t) and (vy, t) diagrams for a body of unit mass. Find the force as a function of time.
 (a) |
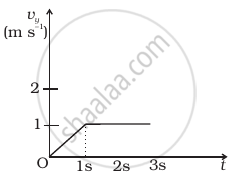 (b) |
