Advertisements
Advertisements
प्रश्न
Find the area of a trapezium whose parallel sides are of length 16 dm and 22 dm and whose height is 12 dm.
उत्तर
Given:
Lengths of the parallel sides are 16 dm and 22 dm.
And, height between the parallel sides is 12 dm.
Area of trapezium \[\frac{1}{2}\times(\text{ Sum of the parallel sides })\times(\text{ Height })\]
\[ = \frac{1}{2} \times (16 + 22) \times (12)\]
\[ {=228 dm}^2 \]
\[ = 228 \times dm\times dm\]
\[=228\times\frac{1}{10}m\times\frac{1}{10}m\]
\[ = 2 . 28 m^2\]
APPEARS IN
संबंधित प्रश्न
The area of a trapezium is 960 cm2. If the parallel sides are 34 cm and 46 cm, find the distance between them.
Find the area enclosed by each of the following figures [Fig. 20.49 (i)-(iii)] as the sum of the areas of a rectangle and a trapezium: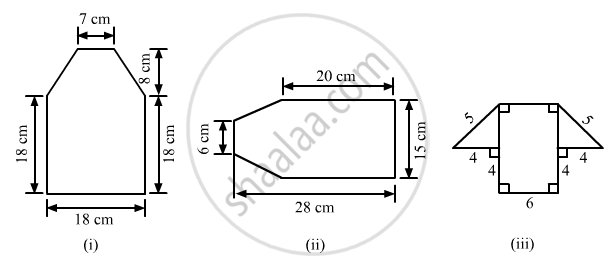
There is a pentagonal shaped park as shown in Fig. 20.50. Jyoti and Kavita divided it in two different ways.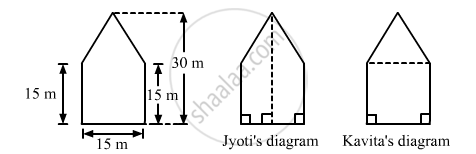
Find the area of this park using both ways. Can you suggest some another way of finding its areas?
☐ PQRS is an isosceles trapezium l(PQ) = 7 cm. seg PM ⊥ seg SR, l(SM) = 3 cm, Distance between two parallel sides is 4 cm, find the area of ☐ PQRS.
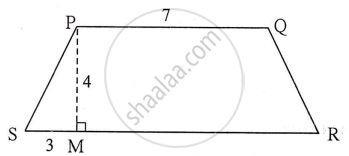
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 16 cm | 15 cm | 360 sq.cm |
Find the area of a trapezium whose parallel sides are 24 cm and 20 cm and the distance between them is 15 cm
The area of a trapezium is 1080 sq.cm. If the lengths of its parallel sides are 55.6 cm and 34.4 cm. Find the distance between them
The sunshade of a window is in the form of isosceles trapezium whose parallel sides are 81 cm and 64 cm and the distance between them is 6 cm. Find the cost of painting the surface at the rate of ₹ 2 per sq.cm
The area of the trapezium, if the parallel sides are measuring 8 cm and 10 cm and the height 5 cm is
The area of a trapezium become 4 times if its height gets doubled.
