Advertisements
Advertisements
प्रश्न
Find the area of a trapezium whose parallel sides of lengths 10 cm and 15 cm are at a distance of 6 cm from each other. Calculate this area as the difference of the area of a rectangle and the sum of the areas of two triangles.
उत्तर
Given:
Length of the parallel sides of a trapezium are 10 cm and 15 cm.
The distance between them is 6 cm.
Let us extend the smaller side and then draw perpendiculars from the ends of both sides.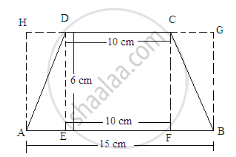
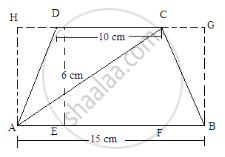
Area of trapezium ABCD=(Area of rectangle ABGH)-[(Area of triangle AHD)+(Area of triangle BGC)]
\[ = (15 \times 6) - [(\frac{1}{2} \times DH \times 6) + (\frac{1}{2} \times GC \times 6)]\]
\[ = 90 - [3\times DH + 3 \times GC]\]
= 90 - 3[DH+GC]
Here, HD+DC+CG=15 cm
DC=10 cm
HD+10+CG=15
HD+GC=15-10=5 cm
Putting this value in the above equation:
\[ {\text{ Area of the trapezium }=90-3(5)=90-15=75 cm}^2\]
APPEARS IN
संबंधित प्रश्न
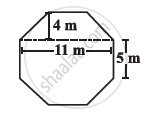
Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
Find the area, in square metres, of the trapezium whose bases and altitude is as under:
bases = 8 m and 60 dm, altitude = 40 dm
Find the sum of the lengths of the bases of a trapezium whose area is 4.2 m2 and whose height is 280 cm.
If the area of a trapezium is 28 cm2 and one of its parallel sides is 6 cm, find the other parallel side if its altitude is 4 cm.
The following figure shows the cross-section ABCD of a swimming pool which is a trapezium in shape.
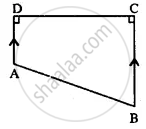
If the width DC, of the swimming pool, is 6.4 m, depth (AD) at the shallow end is 80 cm and depth (BC) at the deepest end is 2.4 m, find its area of the cross-section.
Find the area of the trapezium ABCD in which AB || DC, AB = 18 cm, ∠B = ∠C = 90°, CD = 12 cm and AD = 10 cm.
The area of a trapezium is 1586 sq.cm. The distance between its parallel sides is 26 cm. If one of the parallel sides is 84 cm then find the other side
In a trapezium if the sum of the parallel sides is 10 cm and the area is 140 sq.cm, then the height is
A trapezium with 3 equal sides and one side double the equal side can be divided into ______ equilateral triangles of ______ area.
The area of a trapezium with equal non-parallel sides is 168 m2. If the lengths of the parallel sides are 36 m and 20 m, find the length of the non-parallel sides.
