Advertisements
Advertisements
Question
Find the area of a trapezium whose parallel sides of lengths 10 cm and 15 cm are at a distance of 6 cm from each other. Calculate this area as the difference of the area of a rectangle and the sum of the areas of two triangles.
Solution
Given:
Length of the parallel sides of a trapezium are 10 cm and 15 cm.
The distance between them is 6 cm.
Let us extend the smaller side and then draw perpendiculars from the ends of both sides.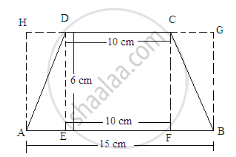
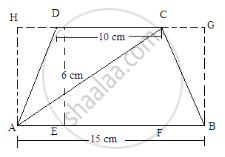
Area of trapezium ABCD=(Area of rectangle ABGH)-[(Area of triangle AHD)+(Area of triangle BGC)]
\[ = (15 \times 6) - [(\frac{1}{2} \times DH \times 6) + (\frac{1}{2} \times GC \times 6)]\]
\[ = 90 - [3\times DH + 3 \times GC]\]
= 90 - 3[DH+GC]
Here, HD+DC+CG=15 cm
DC=10 cm
HD+10+CG=15
HD+GC=15-10=5 cm
Putting this value in the above equation:
\[ {\text{ Area of the trapezium }=90-3(5)=90-15=75 cm}^2\]
APPEARS IN
RELATED QUESTIONS
Find the area, in square metres, of the trapezium whose bases and altitude is as under:
bases = 12 dm and 20 dm, altitude = 10 dm
Find the area, in square metres, of the trapezium whose bases and altitude is as under:
bases = 8 m and 60 dm, altitude = 40 dm
Find the sum of the lengths of the bases of a trapezium whose area is 4.2 m2 and whose height is 280 cm.
The area of a trapezium is 384 cm2. Its parallel sides are in the ratio 3 : 5 and the perpendicular distance between them is 12 cm. Find the length of each one of the parallel sides.
In Fig. 20.38, a parallelogram is drawn in a trapezium, the area of the parallelogram is 80 cm2, find the area of the trapezium.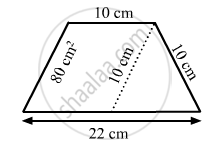
The area of a trapezium is 279 sq.cm and the distance between its two parallel sides is 18 cm. If one of its parallel sides is longer than the other side by 5 cm, find the lengths of its parallel sides.
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 13 cm | 28 cm | 492 sq.cm |
In a trapezium if the sum of the parallel sides is 10 cm and the area is 140 sq.cm, then the height is
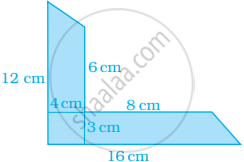
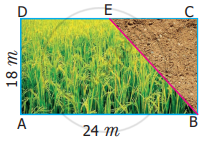
Arivu has a land ABCD with the measurements given in the figure. If a portion ABED is used for cultivation (where E is the mid-point of DC), find the cultivated area.
Find the area of the shaded portion in the following figure.