Advertisements
Advertisements
Question
The area of a trapezium is 384 cm2. Its parallel sides are in the ratio 3 : 5 and the perpendicular distance between them is 12 cm. Find the length of each one of the parallel sides.
Solution
Area of the trapezium = 384 cm2
The parallel sides are in the ratio 3:5 and the perpendicular height between them is 12 cm.
Suppose that the sides are in x multiples of each other.
Then, length of the shorter side = 3x
Length of the longer side = 5x
Area of a trapezium \[=\frac{1}{2}\times(\text{ Sum of parallel sides })\times(\text{ Height })\]
\[ \Rightarrow 384 = \frac{1}{2} \times (3x+5x)\times(12)\]
\[ \Rightarrow 384=\frac{12}{2}\times(8x)\]
\[ \Rightarrow 384=6\times(8x)\]
\[ \Rightarrow 8x = \frac{384}{6}=64\]
\[ \Rightarrow x=\frac{64}{8}=8 cm\]
\[ \therefore\text{ Length of the shorter side }=3\times x=3\times 8=24 cm\]
\[\text{ And, length of the longer side }=5\times x=5\times 8 =40 cm\]
APPEARS IN
RELATED QUESTIONS
Find the sum of the lengths of the bases of a trapezium whose area is 4.2 m2 and whose height is 280 cm.
Find the area of a trapezium whose parallel sides of lengths 10 cm and 15 cm are at a distance of 6 cm from each other. Calculate this area as
the sum of the areas of two triangles and one rectangle.
Find the area of Fig. as the sum of the areas of two trapezium and a rectangle.
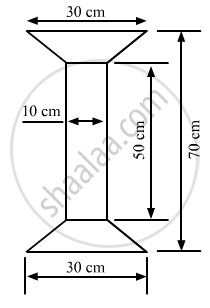
Find the area of a trapezium whose parallel sides are 25 cm, 13 cm and the other sides are 15 cm each.
In Fig. 20.38, a parallelogram is drawn in a trapezium, the area of the parallelogram is 80 cm2, find the area of the trapezium.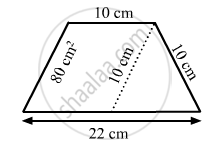
The area of a trapezium is 279 sq.cm and the distance between its two parallel sides is 18 cm. If one of its parallel sides is longer than the other side by 5 cm, find the lengths of its parallel sides.
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 10 m | 12 m | 20 m |
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 13 cm | 28 cm | 492 sq.cm |
The sunshade of a window is in the form of isosceles trapezium whose parallel sides are 81 cm and 64 cm and the distance between them is 6 cm. Find the cost of painting the surface at the rate of ₹ 2 per sq.cm
The area of a trapezium become 4 times if its height gets doubled.
