Advertisements
Advertisements
Question
Find the area of a trapezium whose parallel sides are 25 cm, 13 cm and the other sides are 15 cm each.
Solution
Given:
Parallel sides of a trapezium are 25 cm and 13 cm.
Its nonparallel sides are equal in length and each is equal to 15 cm.
A rough skech of the trapezium is given below:\
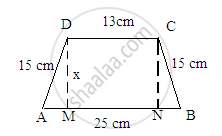
In above figure, we observe that both the right angle triangles AMD and BNC are similar triangles.
This is because both have two common sides as 15 cm and the altitude as x and a right angle.
Hence, the remaining side of both the triangles will be equal.
∴ AM=BN
Also MN=13
Now, since AB=AM+MN+NB:
∴ 25=AM+13+BN
AM+BN=25-13=12 cm
Or, BN+BN=12 cm (Because AM=BN)
2 BN=12
\[BN=\frac{12}{2} = 6cm\]
∴ AM=BN=6 cm
Now, to find the value of x, we will use the Pythagorian theorem in the right angle triangle AMD whose sides are 15, 6 and x.
\[ {(\text{ Hypotenus })}^2 = (\text{ Base })^2 + (\text{ Altitude })^2 \]
\[(15 )^2 = (6 )^2 + (x)2\]
\[225 = 36 + x^2 \]
\[ x^2 = 225 - 36 = 189\]
\[ \therefore x =\sqrt{189}=\sqrt{9 \times 21}= 3\sqrt{21}cm\]
\[ \therefore\text{ Distance between the parallel sides }=3\sqrt{21} cm\]
\[ \therefore\text{ Area of trapezium }=\frac{1}{2} \times(\text{ Sum of parallel sides })\times(\text{ Distance between the parallel sides })\]
\[ = \frac{1}{2} \times(25+13)\times( 3\sqrt{21})\]
\[ = 57\sqrt{21} {cm}^2\]
APPEARS IN
RELATED QUESTIONS
The area of a trapezium is 34 cm2 and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.
Find the area of trapezium with base 15 cm and height 8 cm, if the side parallel to the given base is 9 cm long.
Top surface of a table is trapezium in shape. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.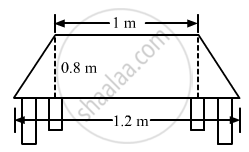
The area of a trapezium is 1586 cm2 and the distance between the parallel sides is 26 cm. If one of the parallel sides is 38 cm, find the other.
The parallel sides of a trapezium are 25 cm and 13 cm; its nonparallel sides are equal, each being 10 cm, find the area of the trapezium.
If the area of a trapezium is 28 cm2 and one of its parallel sides is 6 cm, find the other parallel side if its altitude is 4 cm.
In Fig. 20.38, a parallelogram is drawn in a trapezium, the area of the parallelogram is 80 cm2, find the area of the trapezium.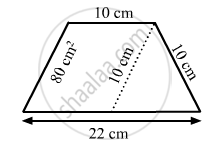
Find the area of the pentagon shown in fig. 20.48, if AD = 10 cm, AG = 8 cm, AH = 6 cm, AF = 5 cm, BF = 5 cm, CG = 7 cm and EH = 3 cm.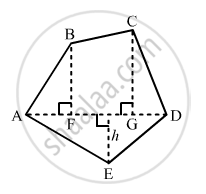
The parallel sides of a trapezium are in ratio 3: 4. If the distance between the parallel sides is 9 dm and its area is 126 dm2; find the lengths of its parallel sides.
The area of a trapezium become 4 times if its height gets doubled.
