Advertisements
Advertisements
Question
The parallel sides of a trapezium are 25 cm and 13 cm; its nonparallel sides are equal, each being 10 cm, find the area of the trapezium.
Solution
Given:
The parallel sides of a trapezium are 25 cm and 13 cm.
Its nonparallel sides are equal in length and each is equal to 10 cm.
A rough sketch for the given trapezium is given below: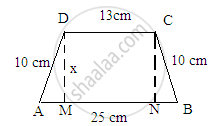
In above figure, we observe that both the right angle trangles AMD and BNC are congruent triangles.
AD = BC = 10 cm
D = CN = x cm
\[\angle DMA = \angle CNB = 90^\circ\]
Hence, the third side of both the triangles will also be equal.
\[ \therefore AM=BN\]
Also, MN=13
Since AB = AM+MN+NB:
\[ \therefore 25=AM+13+BN\]
\[AM+BN=25-13=12 cm\]
\[Or, BN+BN=12 cm (\text{ Because AM=BN })\]
\[2 BN=12\]
\[BN=\frac{12}{2}=6 cm\]
∴ AM = BN = 6 cm.
Now, to find the value of x, we will use the Pythagoras theorem in the right angle triangle AMD, whose sides are 10, 6 and x.
\[ {(\text{ Hypotenuse })}^2 {=(\text{ Base })}^2 {+(\text{ Altitude })}^2 \]
\[ {(10)}^2 {=(6)}^2 {+(x)}^2 \]
\[ {100=36+x}^2 \]
\[ x^2 =100-36=64\]
\[x=\sqrt{64}=8 cm\]
∴ Distance between the parallel sides = 8 cm
∴ Area of trapezium\[=\frac{1}{2}\times( \text{ Sum of parallel sides })\times(\text{ Distance between parallel sides })\]
\[=\frac{1}{2}\times(25+13)\times(8)\]
\[ {=152 cm}^2\]
APPEARS IN
RELATED QUESTIONS
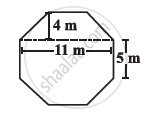
Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
Find the sum of the lengths of the bases of a trapezium whose area is 4.2 m2 and whose height is 280 cm.
Mohan wants to buy a trapezium shaped field. Its side along the river is parallel and twice the side along the road. If the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.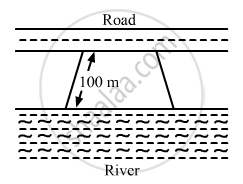
In Fig. 20.38, a parallelogram is drawn in a trapezium, the area of the parallelogram is 80 cm2, find the area of the trapezium.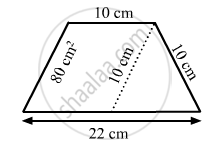
The two parallel sides and the distance between them are in the ratio 3: 4: 2. If the area of the trapezium is 175 cm2, find its height.
The area of a trapezium is 279 sq.cm and the distance between its two parallel sides is 18 cm. If one of its parallel sides is longer than the other side by 5 cm, find the lengths of its parallel sides.
The sunshade of a window is in the form of isosceles trapezium whose parallel sides are 81 cm and 64 cm and the distance between them is 6 cm. Find the cost of painting the surface at the rate of ₹ 2 per sq.cm
A window is in the form of trapezium whose parallel sides are 105 cm and 50 cm respectively and the distance between the parallel sides is 60 cm. Find the cost of the glass used to cover the window at the rate of ₹ 15 per 100 sq.cm
The perimeter of a trapezium is 52 cm and its each non-parallel side is equal to 10 cm with its height 8 cm. Its area is ______.
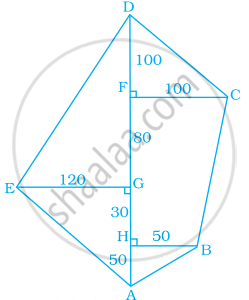
Find the area of the following fields. All dimensions are in metres.