Advertisements
Advertisements
प्रश्न
The parallel sides of a trapezium are 25 cm and 13 cm; its nonparallel sides are equal, each being 10 cm, find the area of the trapezium.
उत्तर
Given:
The parallel sides of a trapezium are 25 cm and 13 cm.
Its nonparallel sides are equal in length and each is equal to 10 cm.
A rough sketch for the given trapezium is given below: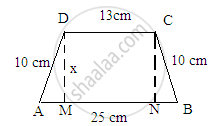
In above figure, we observe that both the right angle trangles AMD and BNC are congruent triangles.
AD = BC = 10 cm
D = CN = x cm
\[\angle DMA = \angle CNB = 90^\circ\]
Hence, the third side of both the triangles will also be equal.
\[ \therefore AM=BN\]
Also, MN=13
Since AB = AM+MN+NB:
\[ \therefore 25=AM+13+BN\]
\[AM+BN=25-13=12 cm\]
\[Or, BN+BN=12 cm (\text{ Because AM=BN })\]
\[2 BN=12\]
\[BN=\frac{12}{2}=6 cm\]
∴ AM = BN = 6 cm.
Now, to find the value of x, we will use the Pythagoras theorem in the right angle triangle AMD, whose sides are 10, 6 and x.
\[ {(\text{ Hypotenuse })}^2 {=(\text{ Base })}^2 {+(\text{ Altitude })}^2 \]
\[ {(10)}^2 {=(6)}^2 {+(x)}^2 \]
\[ {100=36+x}^2 \]
\[ x^2 =100-36=64\]
\[x=\sqrt{64}=8 cm\]
∴ Distance between the parallel sides = 8 cm
∴ Area of trapezium\[=\frac{1}{2}\times( \text{ Sum of parallel sides })\times(\text{ Distance between parallel sides })\]
\[=\frac{1}{2}\times(25+13)\times(8)\]
\[ {=152 cm}^2\]
APPEARS IN
संबंधित प्रश्न
Find the area, in square metres, of the trapezium whose bases and altitude is as under:
bases = 8 m and 60 dm, altitude = 40 dm
Find the area of a trapezium whose parallel sides of lengths 10 cm and 15 cm are at a distance of 6 cm from each other. Calculate this area as
the sum of the areas of two triangles and one rectangle.
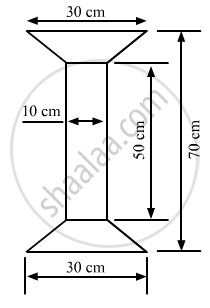
Find the area of Fig. as the sum of the areas of two trapezium and a rectangle.
The area of a trapezium is 91 cm2 and its height is 7 cm. If one of the parallel sides is longer than the other by 8 cm, find the two parallel sides.
The area of a trapezium is 1586 cm2 and the distance between the parallel sides is 26 cm. If one of the parallel sides is 38 cm, find the other.
Find the area of the pentagon shown in fig. 20.48, if AD = 10 cm, AG = 8 cm, AH = 6 cm, AF = 5 cm, BF = 5 cm, CG = 7 cm and EH = 3 cm.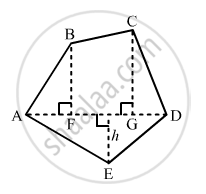
Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm respectively and its height is 4.2 cm, find its area.
The parallel sides of a trapezium are in ratio 3: 4. If the distance between the parallel sides is 9 dm and its area is 126 dm2; find the lengths of its parallel sides.
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 16 cm | 15 cm | 360 sq.cm |
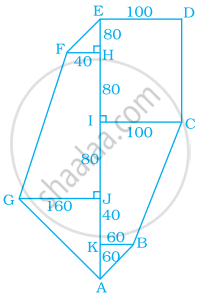
Find the area of the following fields. All dimensions are in metres.