Advertisements
Advertisements
प्रश्न
Find the area of the following fields. All dimensions are in metres.
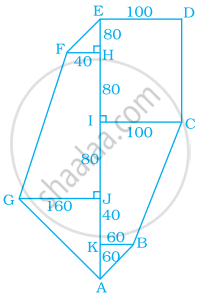
उत्तर
Area of the given figure
= Area of ΔEFH + Area of rectangle EDCI + Area of trapezium FHJG + Area of trapezium ICBK + Area of ΔGJA + Area of ΔKBA
Area of ΔEFH = `1/2 xx "Base" xx "Height"`
= `1/2 xx 40 xx 80`
= 40 × 40
= 1600 m2
Area of rectangle EDCI = Length × Breadth = 100 × 160 = 16000 m2
Area of trapezium FHJG = `1/2` × [Sum of parallel sides] × Height
= `1/2 xx [40 + 160] xx 160`
= `200/2 xx 160`
= 100 × 160
= 16000 m2
Area of trapezium ICBK = `1/2` × [Sum of parallel sides] × Height
= `1/2 xx [60 + 100] xx 120`
= `1/2 xx 160 xx 120`
= 80 × 120
= 9600 m2
Area of ΔAJG = `1/2` × Base × Height
= `1/2 xx 160 xx 100`
= 80 × 100
= 8000 m2
Area of ΔKBA = `1/2` × Base × Height
= `1/2 xx 60 xx 60`
= 60 × 30
= 1800 m2
Thus, the area of the complete figure
= 1600 + 16000 + 16000 + 9600 + 8000 + 1800
= 53000 m2
APPEARS IN
संबंधित प्रश्न
Find the area of trapezium with base 15 cm and height 8 cm, if the side parallel to the given base is 9 cm long.
Find the area of a trapezium whose parallel sides are of length 16 dm and 22 dm and whose height is 12 dm.
Find the altitude of a trapezium whose area is 65 cm2 and whose bases are 13 cm and 26 cm.
Find the sum of the lengths of the bases of a trapezium whose area is 4.2 m2 and whose height is 280 cm.
Find the area of a trapezium whose parallel sides of lengths 10 cm and 15 cm are at a distance of 6 cm from each other. Calculate this area as
the sum of the areas of two triangles and one rectangle.
The area of a trapezium is 960 cm2. If the parallel sides are 34 cm and 46 cm, find the distance between them.
Find the area of the field shown in Fig. 20.39 by dividing it into a square, a rectangle and a trapezium.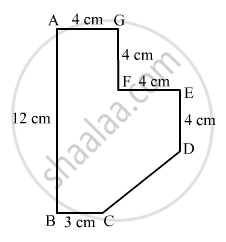
The sunshade of a window is in the form of isosceles trapezium whose parallel sides are 81 cm and 64 cm and the distance between them is 6 cm. Find the cost of painting the surface at the rate of ₹ 2 per sq.cm
The area of a trapezium with equal non-parallel sides is 168 m2. If the lengths of the parallel sides are 36 m and 20 m, find the length of the non-parallel sides.
The areas of two circles are in the ratio 49 : 64. Find the ratio of their circumferences.
