Advertisements
Advertisements
प्रश्न
The areas of two circles are in the ratio 49 : 64. Find the ratio of their circumferences.
उत्तर
Given, the area of two circles are in the ratio 49 : 64
Area of a circle = πr2
Let area of the first circle = `pir_1^2`
And area of the second circle = `pir_2^2`
According to the question,
`49/64 = (pir_1^2)/(pir_2^2)`
⇒ `49/64 = r_1^2/r_2^2`
⇒ `(7)^2/(8)^2 = r_1^2/r_2^2`
⇒ `(7/8)^2 = (r_1/r_2)^2`
∴ r1 = 7 and r2 = 8
The ratio of circumferences of these two circles
= `(2pir_1)/(2pir_2)` ...[∵ Circumference of circle = 2πr]
= `r_1/r_2`
= `7/8`
Hence, required ratio is 7 : 8
APPEARS IN
संबंधित प्रश्न
The area of a trapezium is 960 cm2. If the parallel sides are 34 cm and 46 cm, find the distance between them.
Top surface of a table is trapezium in shape. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.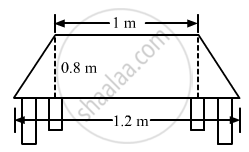
The parallel sides of a trapezium are in ratio 3: 4. If the distance between the parallel sides is 9 dm and its area is 126 dm2; find the lengths of its parallel sides.
The two parallel sides and the distance between them are in the ratio 3: 4: 2. If the area of the trapezium is 175 cm2, find its height.
The area of a trapezium is 279 sq.cm and the distance between its two parallel sides is 18 cm. If one of its parallel sides is longer than the other side by 5 cm, find the lengths of its parallel sides.
Find the area of the trapezium ABCD in which AB || DC, AB = 18 cm, ∠B = ∠C = 90°, CD = 12 cm and AD = 10 cm.
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 10 m | 12 m | 20 m |
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 13 cm | 28 cm | 492 sq.cm |
The area of a trapezium is 180 sq.cm and its height is 9 cm. If one of the parallel sides is longer than the other by 6 cm. Find the length of the parallel sides.
When the non-parallel sides of a trapezium are equal then it is known as
