Advertisements
Advertisements
प्रश्न
The areas of two circles are in the ratio 49 : 64. Find the ratio of their circumferences.
उत्तर
Given, the area of two circles are in the ratio 49 : 64
Area of a circle = πr2
Let area of the first circle = `pir_1^2`
And area of the second circle = `pir_2^2`
According to the question,
`49/64 = (pir_1^2)/(pir_2^2)`
⇒ `49/64 = r_1^2/r_2^2`
⇒ `(7)^2/(8)^2 = r_1^2/r_2^2`
⇒ `(7/8)^2 = (r_1/r_2)^2`
∴ r1 = 7 and r2 = 8
The ratio of circumferences of these two circles
= `(2pir_1)/(2pir_2)` ...[∵ Circumference of circle = 2πr]
= `r_1/r_2`
= `7/8`
Hence, required ratio is 7 : 8
APPEARS IN
संबंधित प्रश्न
Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.

Find the area of a trapezium whose parallel sides are of length 16 dm and 22 dm and whose height is 12 dm.
Find the area of Fig. as the sum of the areas of two trapezium and a rectangle.
If the area of a trapezium is 28 cm2 and one of its parallel sides is 6 cm, find the other parallel side if its altitude is 4 cm.
In Fig. 20.38, a parallelogram is drawn in a trapezium, the area of the parallelogram is 80 cm2, find the area of the trapezium.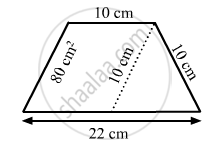
There is a pentagonal shaped park as shown in Fig. 20.50. Jyoti and Kavita divided it in two different ways.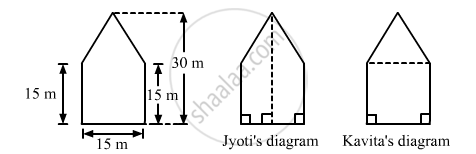
Find the area of this park using both ways. Can you suggest some another way of finding its areas?
The following figure shows the cross-section ABCD of a swimming pool which is a trapezium in shape.
If the width DC, of the swimming pool, is 6.4 m, depth (AD) at the shallow end is 80 cm and depth (BC) at the deepest end is 2.4 m, find its area of the cross-section.
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 10 m | 12 m | 20 m |
A window is in the form of trapezium whose parallel sides are 105 cm and 50 cm respectively and the distance between the parallel sides is 60 cm. Find the cost of the glass used to cover the window at the rate of ₹ 15 per 100 sq.cm
In a trapezium if the sum of the parallel sides is 10 cm and the area is 140 sq.cm, then the height is
