Advertisements
Advertisements
प्रश्न
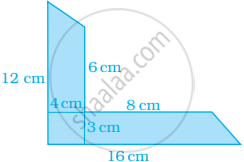
Find the area of Fig. as the sum of the areas of two trapezium and a rectangle.
उत्तर
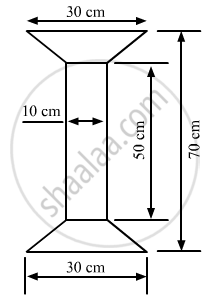
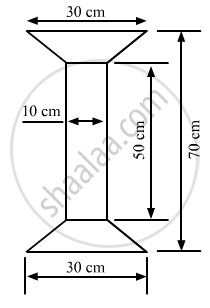
In the given figure, we have a rectangle of length 50 cm and width 10 cm, and two similar trapeziums with parallel sides as 30 cm and 10 cm at both ends.
Suppose x is the perpendicular distance between the parallel sides in both the trapeziums.
We have:
Total length of the given figure = Length of the rectangle + 2 x Perpendicular distancebetween the parallel sides in both the trapeziums
\[70 = 50 + 2 \times x\]
\[2\times x=70-50=20\]
\[x=\frac{20}{2}=10 cm\]
Now, area of the complete figure = (area of the rectangle with sides 50 cm and 10 cm) + 2 x (area of the trapezium with parallel sides 30 cm and 10 cm, and height 10 cm
\[=(50\times10)+2\times[\frac{1}{2}\times(30+10)\times(10)]\]
\[ = 500 + 2 \times [200]\]
= 900 cm2
APPEARS IN
संबंधित प्रश्न
Find the area of a trapezium whose parallel sides are of length 16 dm and 22 dm and whose height is 12 dm.
Find the altitude of a trapezium whose area is 65 cm2 and whose bases are 13 cm and 26 cm.
Find the sum of the lengths of the bases of a trapezium whose area is 4.2 m2 and whose height is 280 cm.
Find the area of a trapezium whose parallel sides of lengths 10 cm and 15 cm are at a distance of 6 cm from each other. Calculate this area as
the sum of the areas of two triangles and one rectangle.
The area of a trapezium is 960 cm2. If the parallel sides are 34 cm and 46 cm, find the distance between them.
Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm respectively and its height is 4.2 cm, find its area.
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 19 m | 16 m | 323 sq.m |
The table top is in the shape of a trapezium with measurements given in the figure. Find the cost of the glass used to cover the table at the rate of ₹ 6 per 10 sq.cm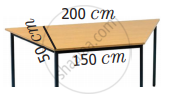
The area of a trapezium become 4 times if its height gets doubled.
Find the area of the shaded portion in the following figure.