Advertisements
Advertisements
प्रश्न
The sunshade of a window is in the form of isosceles trapezium whose parallel sides are 81 cm and 64 cm and the distance between them is 6 cm. Find the cost of painting the surface at the rate of ₹ 2 per sq.cm
उत्तर
Given the parallel sides a = 81 cm, b = 64 cm
Distance between ‘a’ and ‘b’ is height h = 6 cm
Area of the trapezium = `1/2` × h(a + b) sq.units
= `1/2` × 6 × (81 + 64)
= 3 × 145 cm2
= 435 cm2
Cost of painting 1 cm2 = ₹ 2
Cost of painting 435 cm2 = ₹ 435 × 2
= ₹ 870
Cost of painting = ₹ 870.
APPEARS IN
संबंधित प्रश्न
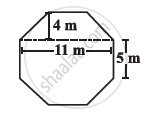
Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
Find the altitude of a trapezium whose area is 65 cm2 and whose bases are 13 cm and 26 cm.
In Fig. 20.38, a parallelogram is drawn in a trapezium, the area of the parallelogram is 80 cm2, find the area of the trapezium.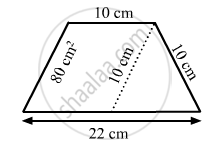
Find the area of the pentagon shown in fig. 20.48, if AD = 10 cm, AG = 8 cm, AH = 6 cm, AF = 5 cm, BF = 5 cm, CG = 7 cm and EH = 3 cm.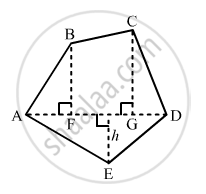
The parallel sides of a trapezium are in ratio 3: 4. If the distance between the parallel sides is 9 dm and its area is 126 dm2; find the lengths of its parallel sides.
The area of a trapezium is 279 sq.cm and the distance between its two parallel sides is 18 cm. If one of its parallel sides is longer than the other side by 5 cm, find the lengths of its parallel sides.
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 16 cm | 15 cm | 360 sq.cm |
Find the area of a trapezium whose parallel sides are 24 cm and 20 cm and the distance between them is 15 cm
The table top is in the shape of a trapezium with measurements given in the figure. Find the cost of the glass used to cover the table at the rate of ₹ 6 per 10 sq.cm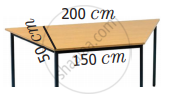
The area of a trapezium become 4 times if its height gets doubled.
