Advertisements
Advertisements
प्रश्न
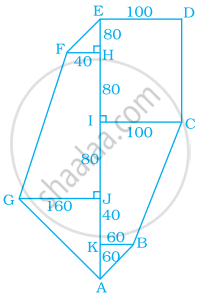
Find the area of the pentagon shown in fig. 20.48, if AD = 10 cm, AG = 8 cm, AH = 6 cm, AF = 5 cm, BF = 5 cm, CG = 7 cm and EH = 3 cm.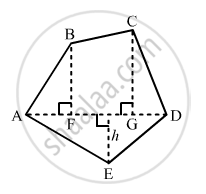
उत्तर
The given figure is:
Given:
AD = 10 cm, AG = 8 cm, AH = 6 cm, AF = 5 cm
BF = 5 cm, CG = 7 cm, EH = 3 cm
∴ FG = AG - AF = 8 - 5 = 3 cm
And, GD = AD - AG = 10 - 8 = 2 cm
From given figure:
Area of Pantagon = (Area of triangle AFB) + (Area of trapezium FBCG) + (Area of triangle CGD) + (Area of triangle ADE)
\[= (\frac{1}{2}\times AF \times BF) + [\frac{1}{2} \times (BF + CG) \times (FG)] + (\frac{1}{2} \times GD \times CG) + (\frac{1}{2}\times AD \times EH)\]
\[=(\frac{1}{2} \times 5 \times 5) + [\frac{1}{2} \times (5 + 7) \times (3)] + (\frac{1}{2} \times 2 \times 7) + (\frac{1}{2}\times 10 \times 3)\]
\[= (\frac{25}{2}) + [\frac{36}{2}] + (\frac{14}{2}) + (\frac{30}{2})\]
\[ = 12 . 5 + 18 + 7 + 15\]
\[ {=52.5 cm}^2\]
APPEARS IN
संबंधित प्रश्न
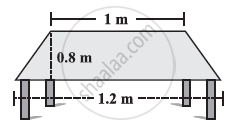
The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.
Find the height of a trapezium, the sum of the lengths of whose bases (parallel sides) is 60 cm and whose area is 600 cm2.
Find the sum of the lengths of the bases of a trapezium whose area is 4.2 m2 and whose height is 280 cm.
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 13 cm | 28 cm | 492 sq.cm |
The sunshade of a window is in the form of isosceles trapezium whose parallel sides are 81 cm and 64 cm and the distance between them is 6 cm. Find the cost of painting the surface at the rate of ₹ 2 per sq.cm
A ground is in the form of isosceles trapezium with parallel sides measuring 42 m and 36 m long. The distance between the parallel sides is 30 m. Find the cost of levelling it at the rate of ₹ 135 per sq.m
The area of a trapezium become 4 times if its height gets doubled.
The area of a trapezium with equal non-parallel sides is 168 m2. If the lengths of the parallel sides are 36 m and 20 m, find the length of the non-parallel sides.
The areas of two circles are in the ratio 49 : 64. Find the ratio of their circumferences.
Find the area of the following fields. All dimensions are in metres.