Advertisements
Advertisements
प्रश्न
Find the area enclosed by each of the following figures [Fig. 20.49 (i)-(iii)] as the sum of the areas of a rectangle and a trapezium: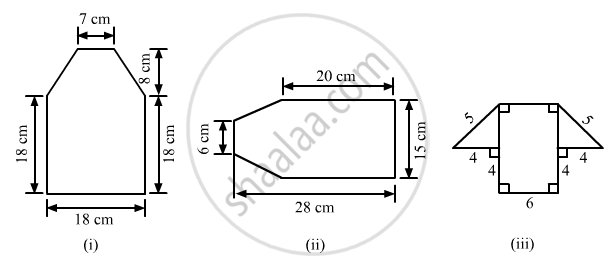
उत्तर
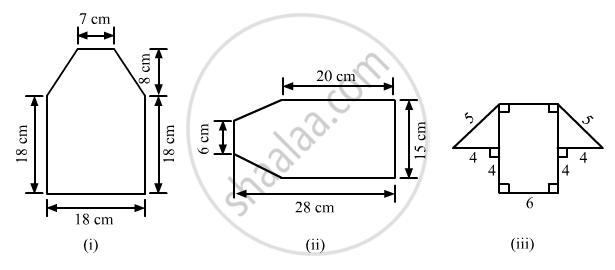 \[(i)\]
\[(i)\]
The given figure can be divided into a rectangle and a trapezium as shown below:
From the above firgure:
Area of the complete figure = (Area of square ABCF)+(Area of trapezium CDEF)
\[=(AB\times BC)+[\frac{1}{2}\times(FC+ED)\times(\text{ Distance between FC and ED })]\]
\[=(18\times18)+[\frac{1}{2}\times(18+7)\times(8)]\]
\[=324+100\]
\[ {=424 cm}^2\]
\[(ii)\]
The given figure can be divided in the following manner:\]
From the above figure:
AB = AC-BC=28-20=8 cm
So that area of the complete figure = (area of rectangle BCDE)+(area of trapezium ABEF)
\[=(BC\times CD)+[\frac{1}{2}\times(BE+AF)\times(AB)]\]
\[=(20\times15)+[\frac{1}{2}\times(15+6)\times(8)]\]
\[=300+84\]
\[ {=384 cm}^2\]
The given figure can be divided in the following manner:
From the above figure:
EF = AB = 6 cm
Now, using the Pythagoras theorem in the right angle triangle CDE:
\[ 5^2 {= 4}^2 {+CE}^2 \]
\[ {CE}^2 = 25-16=9\]
\[CE =\sqrt{9}= 3 cm\]
\[\text{ And, }GD=GH+HC+CD=4+6+4=14 cm\]
\[ \therefore\text{ Area of the complete figure }= (\text{ Area of rectangle ABCH })+(\text{ Area of trapezium GDEF })\]
\[=(AB\times BC)+[\frac{1}{2}\times(GD+EF)\times(CE)]\]
\[=(6\times4)+[\frac{1}{2}\times(14+6)\times(3)]\]
\[=24+30\]
\[ {=54 cm}^2\]
APPEARS IN
संबंधित प्रश्न
Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.

Find the height of a trapezium, the sum of the lengths of whose bases (parallel sides) is 60 cm and whose area is 600 cm2.
The area of a trapezium is 1586 cm2 and the distance between the parallel sides is 26 cm. If one of the parallel sides is 38 cm, find the other.
Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm respectively and its height is 4.2 cm, find its area.
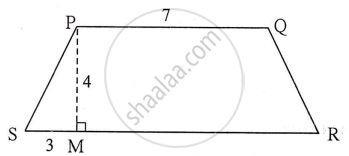
☐ PQRS is an isosceles trapezium l(PQ) = 7 cm. seg PM ⊥ seg SR, l(SM) = 3 cm, Distance between two parallel sides is 4 cm, find the area of ☐ PQRS.
The following figure shows the cross-section ABCD of a swimming pool which is a trapezium in shape.
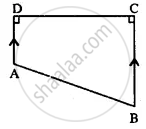
If the width DC, of the swimming pool, is 6.4 m, depth (AD) at the shallow end is 80 cm and depth (BC) at the deepest end is 2.4 m, find its area of the cross-section.
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 19 m | 16 m | 323 sq.m |
The sunshade of a window is in the form of isosceles trapezium whose parallel sides are 81 cm and 64 cm and the distance between them is 6 cm. Find the cost of painting the surface at the rate of ₹ 2 per sq.cm
The area of a trapezium become 4 times if its height gets doubled.
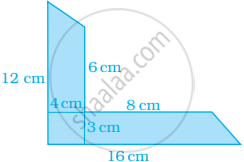
Find the area of the shaded portion in the following figure.